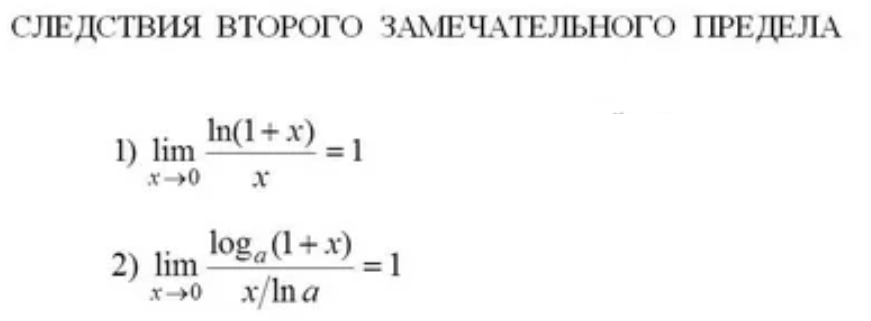Задача 41994 e) lim (x -> 10) (lg(x - 1) / sqrt(x -...
Условие
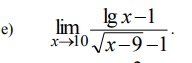
Решение
неопределенность (0/0)
Замена переменной:
x-10=t
x=10+t
lgx-1=lg(10+t)-lg10=lg[m]\frac{10+t}{10}[/m]=lg[m](1+\frac{t}{10})[/m]
sqrt(x-9)-1=sqrt(t+1)-1
[m]\lim_{t \to 0}\frac{lg(1+\frac{t}{10})}{\sqrt{t+1}-1}=[/m]
Умножаем числитель и знаменатель на
sqrt(t+1)+1
[m]\lim_{t \to 0 }\frac{lg(1+\frac{t}{10})(\sqrt{t+1}+1)}{(\sqrt{t+1}-1)(\sqrt{t+1}+1)}=[/m]
[m]=\lim_{t \to 0 }\frac{lg(1+\frac{t}{10})(\sqrt{t+1}+1)}{t}=[/m]
[m]=\lim_{t \to 0 }\frac{lg(1+\frac{t}{10})}{t}\cdot (\sqrt{t+1}+1)=[/m]
предел произведения равен произведению пределов:
[m]=\lim_{t \to 0 }\frac{lg(1+\frac{t}{10})}{t}\cdot\lim_{t \to 0 } (\sqrt{t+1}+1)[/m]
см. приложение ( следствия из второго замеч. предела a=10)
=[m]\frac{ln10}{10}\cdot (\sqrt{1}+1)=\frac{2ln10}{10}[/m]