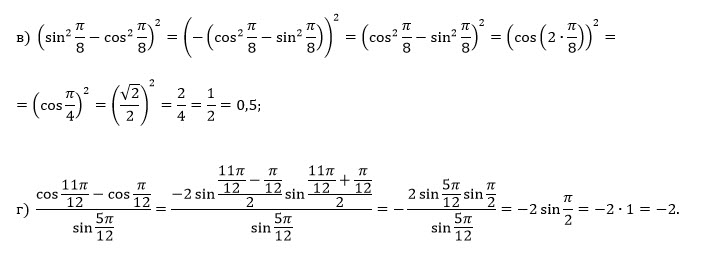Задача 41943 ...

ueisn

2019-11-26 20:19:45

7. Вычислите (без помощи таблиц и калькулятора):

в) (sin² π/8 - cos² π/8)²;

г) (cos 11π/12 - cos π/12)/(sin 5π/12).

sova

2019-11-26 20:57:24

в)
[m]sin^2\frac{\pi }{8}-cos^2\frac{\pi }{8}=-(cos^2\frac{\pi }{8}-sin^2\frac{\pi }{8})=-cos2\cdot\frac{\pi }{8}=-cos\frac{\pi }{4}=-\frac{\sqrt{2}}{2}[/m]

[m](sin^2\frac{\pi }{8}-cos^2\frac{\pi }{8})^2=(-\frac{\sqrt{2}}{2})^2=\frac{1}{2}[/m]

О т в е т. 1/2

г) По формулам приведения:
[m]cos\frac{11\pi }{12}=cos(\pi -\frac{\pi }{12})=-cos\frac{\pi }{12}[/m]



[m]cos\frac{11\pi }{12}-cos\frac{\pi }{12}=cos(\pi -\frac{\pi }{12})-cos\frac{\pi }{12}=-cos\frac{\pi }{12}-cos\frac{\pi }{12}=-2cos\frac{\pi }{12}[/m]


По формулам приведения:

[m]sin\frac{5\pi }{12}=sin(\frac{\pi }{2} -\frac{\pi }{12}) =cos\frac{\pi }{12}[/m]

Итак,
[m]\frac{cos\frac{11\pi }{12}-cos\frac{\pi }{12}}{sin\frac{5\pi }{12}}=\frac{-2cos\frac{\pi }{12}}{cos\frac{\pi }{12}}=-2[/m]

О т в е т. [b]-2[/b]