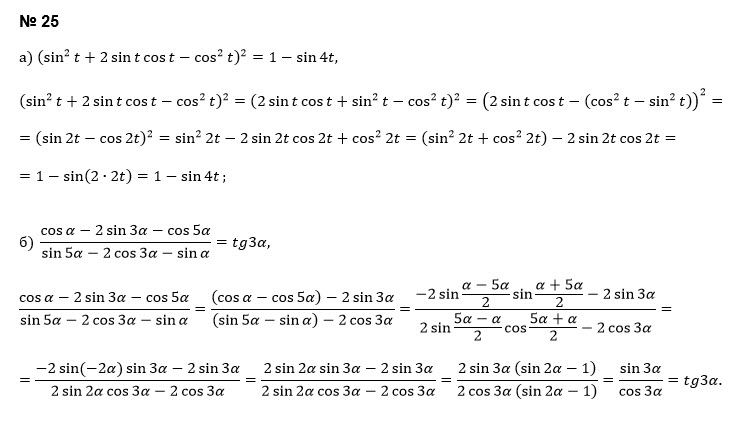Задача 41942 Решите пожалуйста( 25 а, б)...
Условие
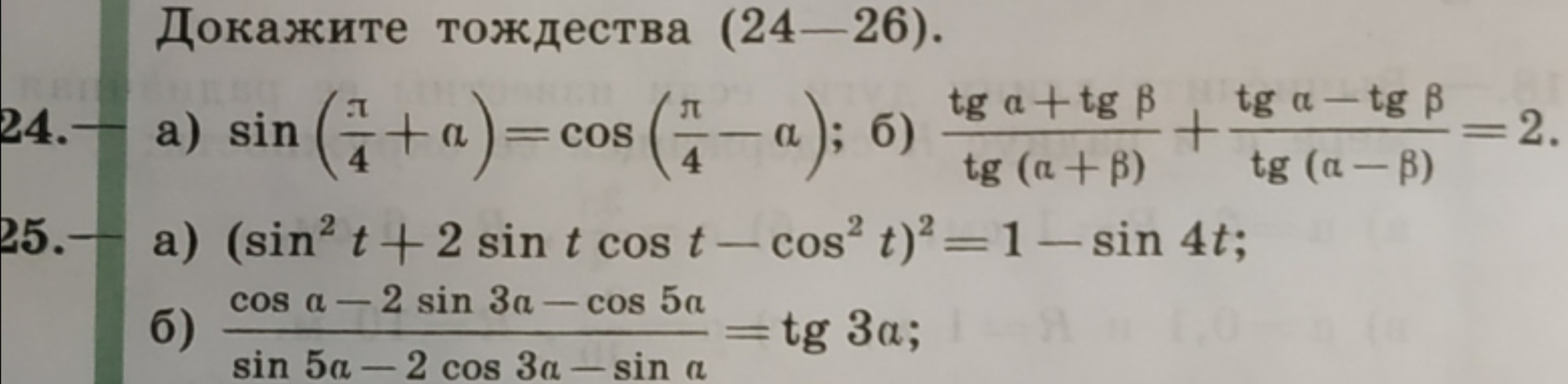
Все решения
т.к.
[green] sin^2t-cos^2t[/green]=-(cos^2t-sin^2t)=[green]-cos2t; [/green]
[blue]2sintcost=sin2t[/blue]
Упрощаем левую часть:
(sin^2t+2sintcost-cos^2t)^2=
=([blue]sin2t[/blue]-[green]cos2t[/green])^2=sin^22t-2sin2t*cos2t+cos^22t=
= (sin^22t+cos^22t)-sin4t=1-sin4t
1-sin4t=1-sin4t ( левая часть равна правой, тождество доказано)
б)
Упрощаем левую часть.
Так как
[m]cos\alpha -cos5\alpha =-2sin\frac{\alpha -5\alpha }{2}\cdot sin\frac{\alpha+5\alpha }{2}=-2sin(-2\alpha) \cdot sin3\alpha =[/m]
[m]=2sin2\alpha) \cdot sin3\alpha[/m]
то числитель:
[b]cos α -2sin3 α -cos5 α [/b]=(cos α -cos5 α )-2sin3 α =
=2sin2 α sin3 α -2sin3 α =2sin3 α *(sin2 α -1)
так как
[m]sin5\alpha -sin\alpha =2sin\frac{5\alpha -\alpha }{2}\cdot cos\frac{5\alpha+\alpha }{2}=2sin2\alpha \cdot cos3\alpha[/m], то
знаменатель
[b]sin5 α -2cos3 α -sin α [/b]=(sin5 α -sin α )-2cos3 α =
=2sin2 α cos3 α -2cos3 α =2cos3 α *(sin2 α -1)
Левая часть
[m]\frac{cos\alpha -2sin3\alpha -cos5\alpha }{sin5\alpha-2cos3\alpha-sin\alpha }=\frac{2sin3\alpha (sin2\alpha -1)}{2cos3\alpha( sin2\alpha -1)}=\frac{sin3\alpha }{cos3\alpha }=tg3\alpha[/m]
tg3 α =tg3 α ( левая часть равна правой части), тождество доказано