Задача 419 Дан треугольник ABC со сторонами AB=15,...
Условие
математика 10-11 класс
9711
Решение
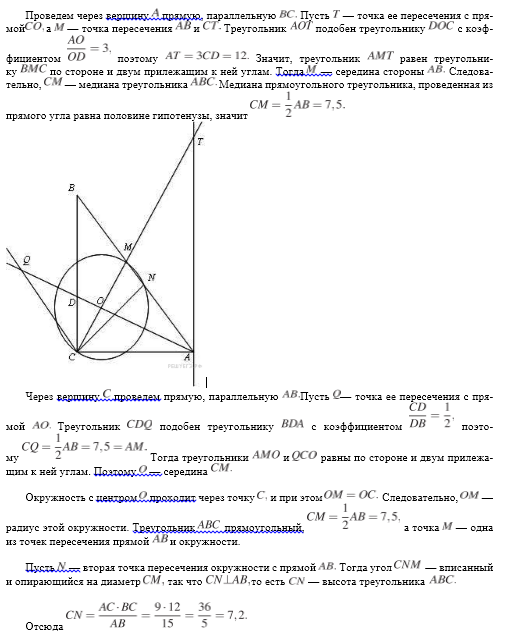
Ответ: 7,5 или 7,2

Ответ: 7,5 или 7,2