Задача 41834 ...

vk306899767

2019-11-23 13:20:21

3.2. Решите уравнение log5(5^x-4) = 1-x.

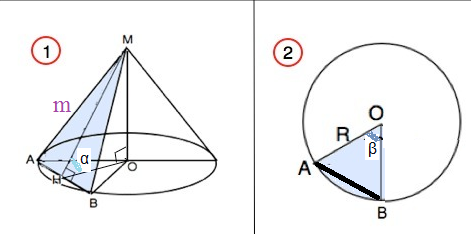
3.3. Через две образующие конуса проведена плоскость, которая наклонена к плоскости его основания под углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра его основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна t.

sova

2019-11-23 13:28:55

★

3.2
По определению логарифма:

5^(1-x)=5^(x)-4

5^(1)*5^(-x)=5^(x)-4

Умножим на 5^(x) > 0

5=5^(x)*5^(x) - 4*5^(x) - квадратное уравнение:

(5^(x))^2-4*(5^(x))-5=0

D=(-4)^2-4*(-5)=36

5^(x)=-1 уравнение не имеет корней, т.к 5^(x) > 0
или
5^(x)=5 ⇒ x=1

О т в е т. 1

3.3

MA=MB=m
∠ MHO= α
∠ AOB= β

Δ AOB - равнобедренный АО=ОВ=R

Пусть [red]R=x[/red]

ОН ⊥ АВ
ОН - [i]высота[/i], [i]медиана[/i] и [i]биссектриса[/i] равнобедренного треугольника Δ AOB,
∠ АОН= ∠ ВОН= β/2

АН=НВ

Из прямоугольного треугольника АОН:
АО=x*sin( β/2) ⇒ AB=2AO=[green]2x*sin( β/2)[/green]
ОН=x*cos( β/2)

Из прямоугольного треугольника МНО:

[b]МO[/b]=ОН*tg α =[blue]x*cos( β/2) *tg α[/blue]

Из прямоугольного треугольника МBО:

МO^2=MB^2-OB^2=m^2-x^2

[b]MO[/b]=[blue]sqrt(m^2-x^2)[/blue]

Уравнение:
[blue]x*cos( β/2) *tg α[/blue][b]=[/b][blue]sqrt(m^2-x^2)[/blue]

Возводим в квадрат, находим x

[red]x=R[/red]

S_(бок)=π*[red]R[/red]*m