Задача 41794 В кубе ABCDA1B1C1D1 с ребром 18...
Условие
Решение
Расстоянием между скрещивающимися прямыми называется [b]расстояние[/b] между [i]одной из скрещивающихся прямых[/i] и [red]плоскостью[/red], проходящей через другую прямую параллельно первой.
Чтобы найти расстояние между двумя скрещивающимися прямыми, нужно:
1. через одну из прямых провести плоскость, параллельную второй прямой.
2. Из любой точки первой прямой опустить перпендикуляр на плоскость и найти его длину.
Первый способ -геометрический
Второй способ - аналитический ( с помощью формулы расстояния от точки до плоскости)
а)
[i]Первый способ[/i] -геометрический
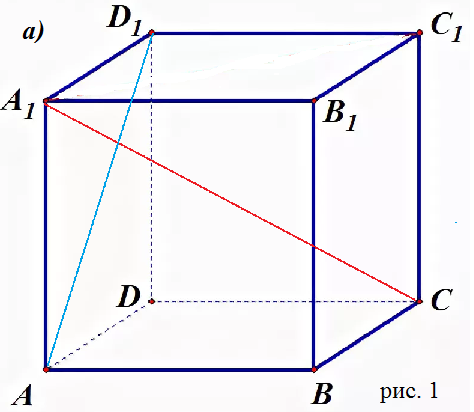
На рис. 1 куб и [i]скрещивающиеся[/i] прямые AD_(1) и А_(1)С ,
расстояние между которыми требуется найти.
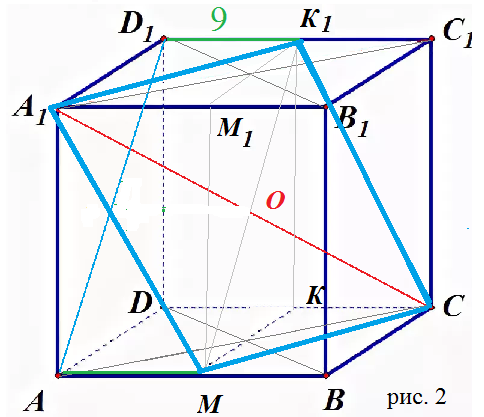
Строим плоскость, проходящую через А_(1)С|| AD_(1).
Проводим MK_(1)
M- cередина АВ
К- середина DC
M_(1) - cередина А_(1)В_(1)
К_(1) - середина D_(1)C_(1)
MK_(1) || AD_(1) ⇒ пл. МА_(1)К_(1)С || AD_(1)
P- cередина AD_(1)
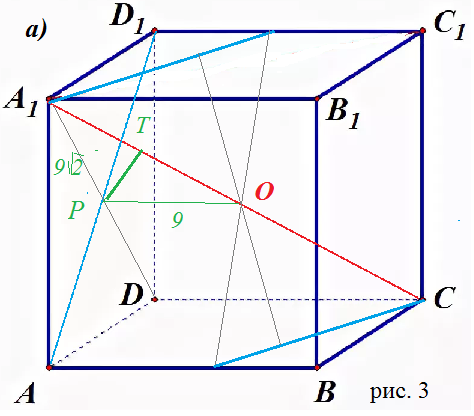
Из точки Р проводим PO || AM
Δ D_(1)PO - прямоугольный.
так как АМ ⊥ пл. АА_(1)D_(1)D ⇒ AM ⊥ AD_(1)
PO|| AM, значит
PO⊥ AD_(1)
Высота PT прямоугольного треугольника Δ D_(1)PO
и есть искомое расстояние.
Как его найти?
По методу площадей.
S_(прямоугольного треуг)=a*b/2 и S_(прямоугольного треуг)=с*h/2
a*b=c*h
h=a*b/c
a=PD_(1)=9sqrt(2)
b=PO=9
c=sqrt(PO^2+PD^2_(1))=9sqrt(3)
h=PT=9*9sqrt(2)/9sqrt(3)=[red]3sqrt(6)[/red]
[i]Второй способ[/i]
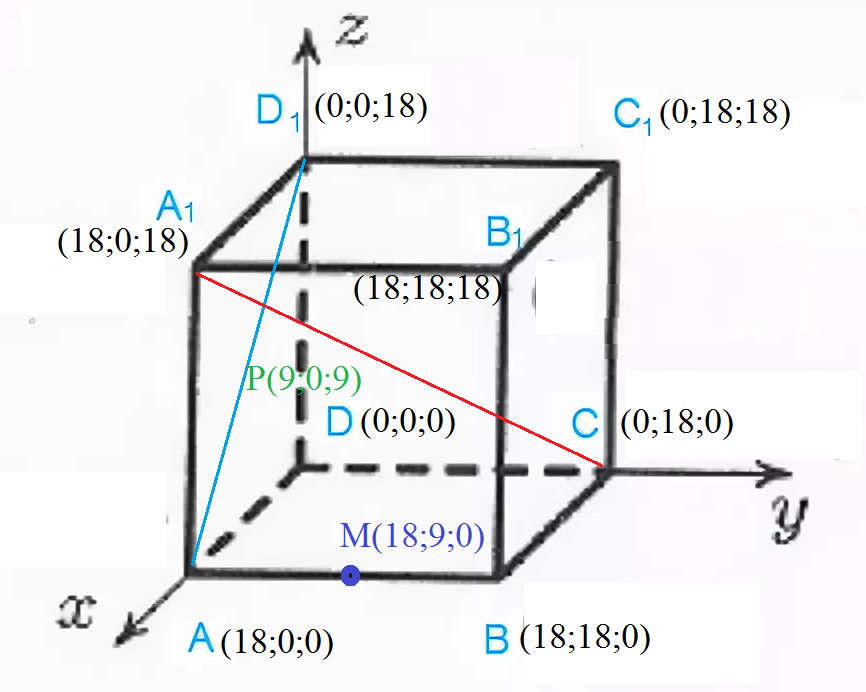
Размещаем куб в системе координат как показано на рисунке.
Составляем уравнение плоскости МА_(1)К_(1)С как плоскости, проходящей через точки:
M(18;9;0)
A_(1)(18;0;18)
C(0;18;0)
[m]\begin{vmatrix} x-18 & y-9 &z \\ 0 &-9 &18 \\ -18& 9 & 0 \end{vmatrix}=0[/m]
-18*18*(y-9)-18*9*z-18*9*(x-18)=0
[b]x+2y+z-36=0[/b]
Расстояние от точки P (9;0;9) до пл.[b]x+2y+z-36=0[/b]
[m]d=\frac{|9+2\cdot 0+9-36|}{\sqrt(1^2+2^2+1^2)}=\frac{18\sqrt{6}}{6}=3\sqrt{6}[/m]
[red]d=3sqrt(6)[/red]
О т в е т ы одинаковые: [red]3sqrt(6)[/red]