Задача 41605 Уравнения линий привести к...
Условие
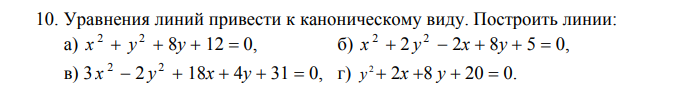
математика ВУЗ
1736
Все решения
x^2+(y^2+8y)+12=0
x^2+(y^2+2*y*4+4^2)-4^2+12=0
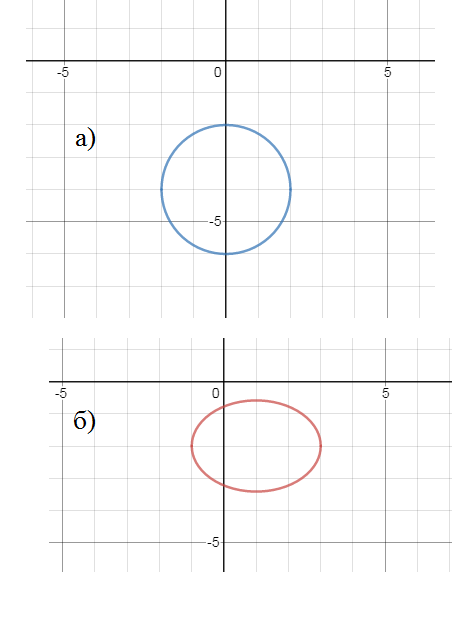
x^2+(y+4)^2=4
(x-0)^2+(y-(-4))^2=2^2
уравнение окружности с центром (0;-4) и радиусом R=2
аналогично
б) (x^2-2x)+(2y^2+8y)+5=0
(x^2-2x+1)-1+2(y^2+4y+4)-8+5=0
(x-1)^2+2*(y+2)^2=4
Делим на 4
[m] \frac{(x-1)^2}{4}+\frac{(y+2)^2}{2}=1[/m]- каноническое уравнение эллипса с центром в точке (1;-2) и полуосями:
большой, равной 2
малой равной sqrt(2)