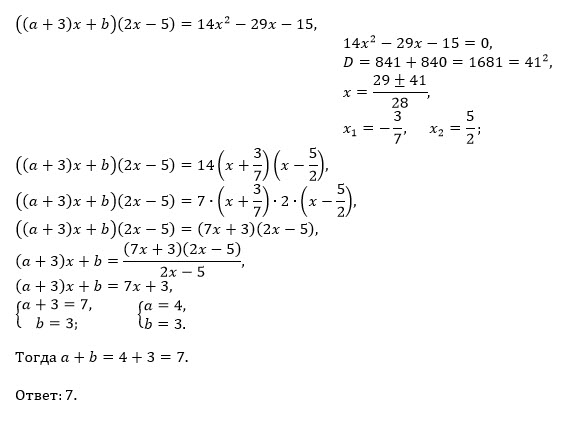Задача 41524 ...

vk556016967

14 ноября 2019 г. в 09:57

Вычислить a+b если ((a+3)x+b)×·2x–5)=14x²–29x–15

sova

14 ноября 2019 г. в 14:24

Раскрываем скобки:
(a+3)x·2x+b·2x+(a+3)x·(–5)+b·(–5)=14x²–29x–15
2(a+3)x²+(–5a–15+2b)x–5b=14x²–29x–15
Два многочлена равны, если равны их степени и равны коэффициенты при одинаковых степенях переменной:

При x²:
2(a+3)=14 ⇒
a+3=7 ⇒
a=4

При x¹:
–5a–15+2b=–29
–5·4–15+2b=–29
2b=6
b=3

При x^o:
–5b=–15 ⇒
b=3

О т в е т. a+b=4+3=7