Задача 41513 Даны три последовательные вершины
УСЛОВИЕ:
1. найти уровень сторон AD
2. уровень высоты опущенной из вершины B на сторону AD
3. найти длину этой высоты
4. уравнение диагонали BD
5. угол между диагоналями параллелограмма
Добавил vk227441747, просмотры: ☺ 700 ⌚ 2019-11-13 16:29:07. математика 4k класс
Решения пользователей
РЕШЕНИЕ ОТ sova
1)
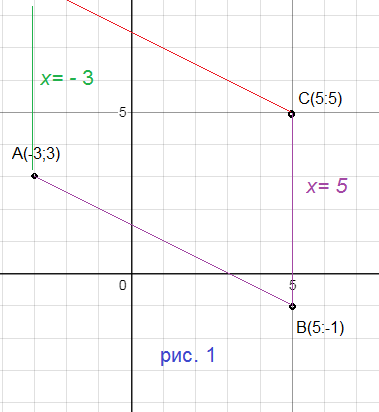
Cм. рис. 1
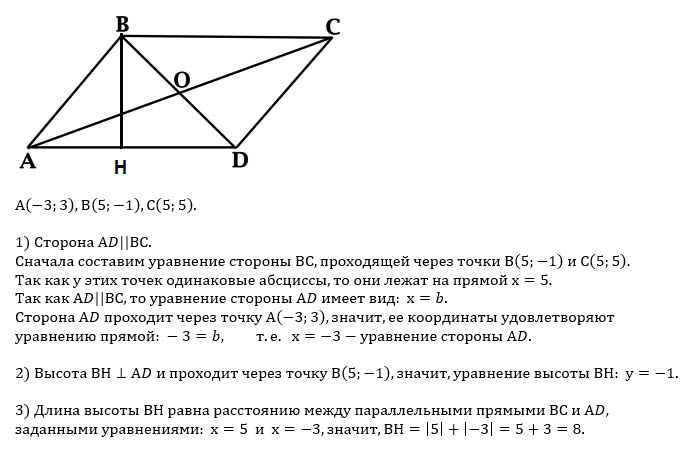
Точки В и С имеют одинаковую первую координату, поэтому [i]уравнение прямой[/i] ВС: [red]х=5[/red]
Прямая AD || BC и проходит через точку А, у которой первая координата равна (-3)
Значит, [i]уравнение прямой[/i] АD:[red] x=-3[/red]
2)
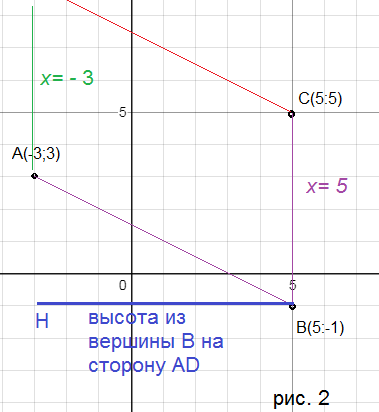
Cм. рис. 2
Высота ВН перпендикулярна AD и значит параллельна оси Ох.
Уравнение прямой, параллельной оси Ох и проходящей через точку В (5;-1)
y=-1
Точка Н - точка пересечения AD и BH
Значит, координаты точки H (-3;-1)
3)
[green]|BH|[/green]=[green]|x_(H)-x_(B)|[/green]=| -3 - 5|= |-8| = 8
так как это частный случай формулы
при y_(H)=y_(B)
|BH|=sqrt((x_(H)-x_(B))^2+(y_(H)-y_(B))^2)=sqrt((x_(H)-x_(B))^2+ (y_(B)-y_(B)^2))=sqrt((x_(H)-x_(B))^2+0)=sqrt((x_(H)-x_(B))^2)=|x_(H)-x_(B)|
4)
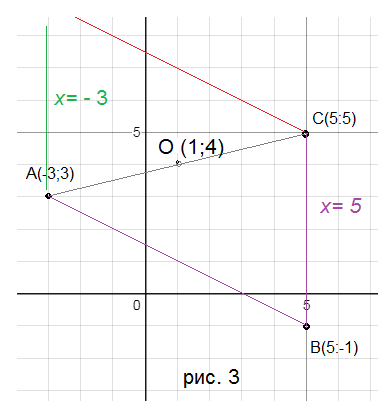
См. рис. 3
Диагонали параллелограмма в точке пересечения делятся пополам.
Координаты точки О как середины отрезка АС:
x_(O)=[m]\frac{x_{A}+x_{B}}{2}=\frac{-3+5}{2}=1[/m]
y_(O)=[m]\frac{y_{A}+y_{B}}{2}=\frac{3+5)}{2}=4[/m]
[blue]O(1; 4)[/blue]
Уравнение диагонали BD - это и уравнение прямой BO.
Составим уравнение применяя общее уравнение прямой, проходящей через две точки
B(5;-1) и О (1; 4)
[m]\frac{x-x_{O}}{x_{B}-x_{O}}=\frac{y-y_{O}}{y_{B}-y_{O}}[/m]
[m]\frac{x-1}{5-1}=\frac{y-4}{-1-4}[/m]
[m]\frac{x-1}{4}=\frac{y-4}{-5}[/m]
Пропорция, перемножаем крайние и средние члены пропорции
-5*(х-1)=4*(у-4)
-5х+5=4у-16
[b]5х+4у-21=0[/b] -[i] уравнение диагонали[/i] BD
5)
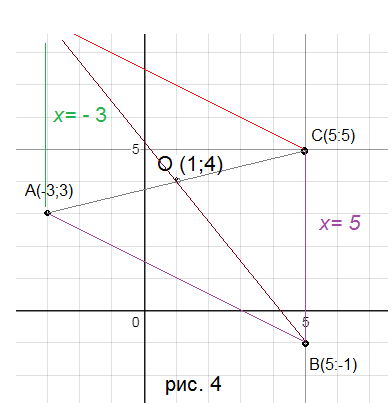
Угол между диагоналями - это меньший из углов, образованных прямыми BO и AC, значит это угол ВОС
Находим его как угол между векторами
vector{OB} и vector{OC}
сos ( ∠ vector{OB}, vector{OC})=[m]\frac{\underset{OB}{\rightarrow}\cdot\underset{OC}{\rightarrow}}{|\underset{OB}{\rightarrow}|\cdot|\underset{OC}{\rightarrow}|}[/m]
Находим координаты векторов
vector{OB}=(5-1;-1-4)=(4;-5)
vector{OC}=(5-1;5-4))=(4;1)
Находим скалярное произведение векторов vector{OB} и vector{OC}
vector{OB}*vector{OC}=4*4+(-5)*1=11
|vector{OB}|=sqrt(4^2+(-5)^2)=sqrt(41)
|vector{OC}|=sqrt(4^2+1^2)=sqrt(17)
сos ( ∠ vector{OB}, vector{OC})=[m]\frac{11}{\sqrt{41}\cdot \sqrt{17}}=\frac{11}{\sqrt{697}}=\frac{11\sqrt{697}}{697}[/m]
Написать комментарий
Если бы не было зависимых слов, то слово писалось бы с одной буквой н
Проведем высоту и медиану СК.
Из Δ АКС:
sin ∠ BAC=CK/AC ⇒ СК=18
По теореме Пифагора:
АК^2=AC^2-CK^2=27^2-18^2
АК=9sqrt(5)
AB=2AK=18sqrt(5)
S_( Δ ABC)=AB*CK/2 и S_( Δ ABC)=BC*AH/2 ⇒
AB*CK=BC*AH ⇒ АН=AB*CK/BC=18sqrt(5)*18/27=12sqrt(5)
Из Δ АBH по теореме Пифагора:
ВН^2=АВ^2-АН^2=(18sqrt(5))^2-(12sqrt(5))^2=5*(18-12)*(18+12)=30^2
[b]ВН=30[/b]
ВН> BC ⇒ ∠ C - [i]тупой[/i] См. рис
Если в литре( 1000мл) 0,1 моль соли, значит в 100 мл в 10 раз меньше - 0,01 моль
Рассчитаем массу 0,01 моль нитрита натрия
m = n*M = 0.01 * 85 = 0.85 г
Таким образом, чтобы получить 100 мл 0,1 М раствора нитрита натрия, нужно взять 0,85 г соли и растворить ее в 100 мл воды
u=x^2+4x+3 ⇒ du=2x+4
dv=e^(2x)dx ⇒ v=(1/2)e^(2x)
∫ (x^2+4x+3)e^(2x) dx=(1/2)e^(2x) *(x^2+4x+3)- ∫ (1/2)e^(2x)*(2x+4)dx=
[b]=(1/2)e^(2x) *(x^2+4x+3)- ∫ e^(2x)*(x+2)dx=[/b]
u=x+2 ⇒ du=dx
dv=e^(2x)dx ⇒ v=(1/2)e^(2x)
[b]=(1/2)e^(2x) *(x^2+4x+3)- ((1/2)e^(2x) *(x+2)-∫ e^(2x)dx=[/b]
[b]=(1/2)e^(2x) *(x^2+4x+3- (1/2)x-1)+(1/2)* e^(2x)+C=[/b]
[b]=(1/2)e^(2x) *(x^2+(7/2)x+3)+C[/b]
log_{0,5}0,5^{1+lgx}\cdot (\frac{5^{1+lgx}}{0,5^{1+lgx}}-1)\leq lgx-1
log_{0,5}0,5^{1+lgx}+log_{0,5}((\frac{5}{0,5})^{1+lgx}-1)\leq lgx-1
1+lgx+log_{0,5}(10^{1+lgx}-1)\leq lgx-1
log_{0,5}(10x-1)\leq -2
log_{0,5}(10x-1)\leq log_{0,5}4
Логарифмическая функция убывает, поэтому
10х-1 ≥ 4
10х ≥ 5
x ≥ 0,5
Удовл ОДЗ
О т в е т. [0,5;+ ∞ )