Задача 41499 Иссследовать один из рядов на сходимость...
Условие
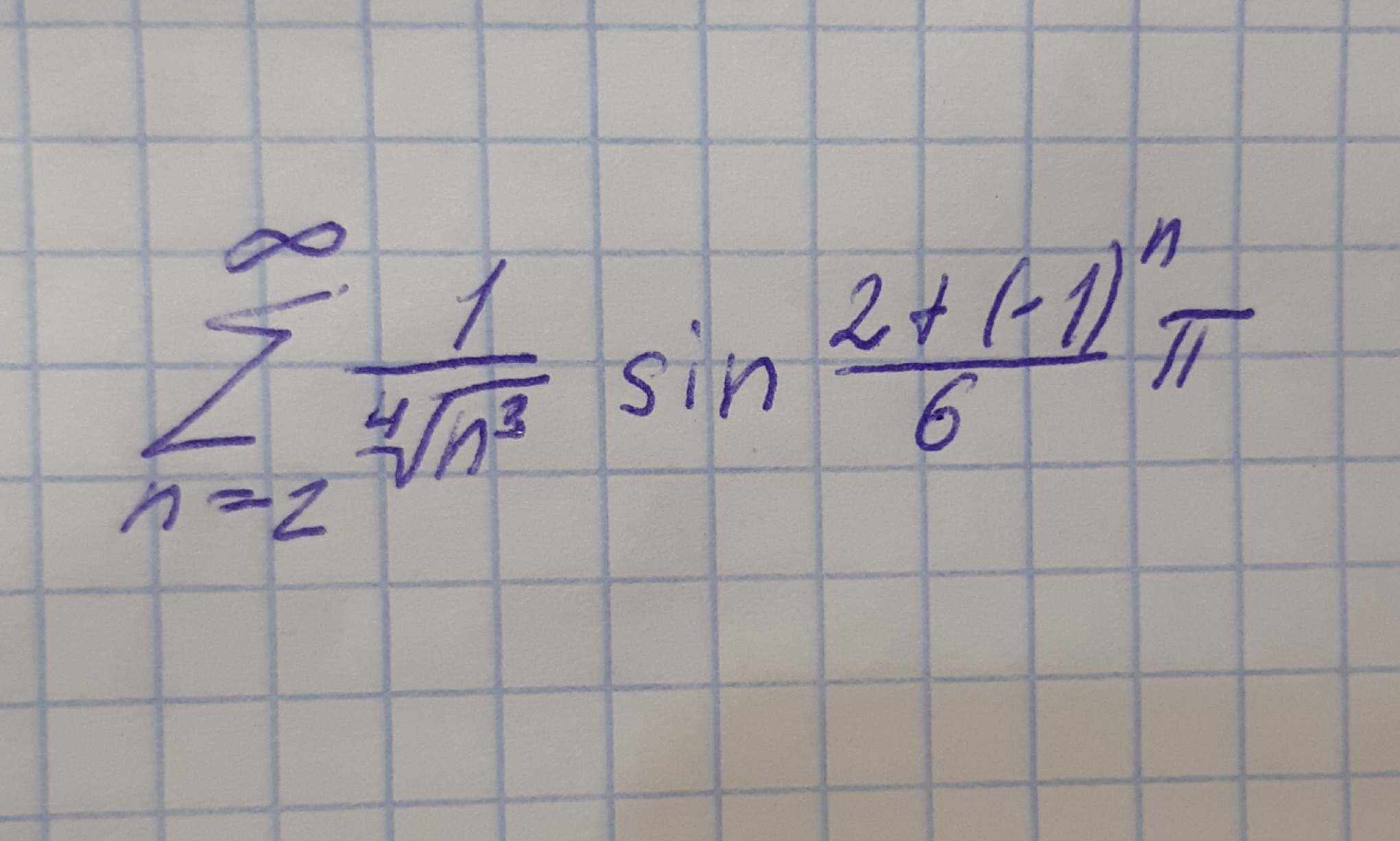
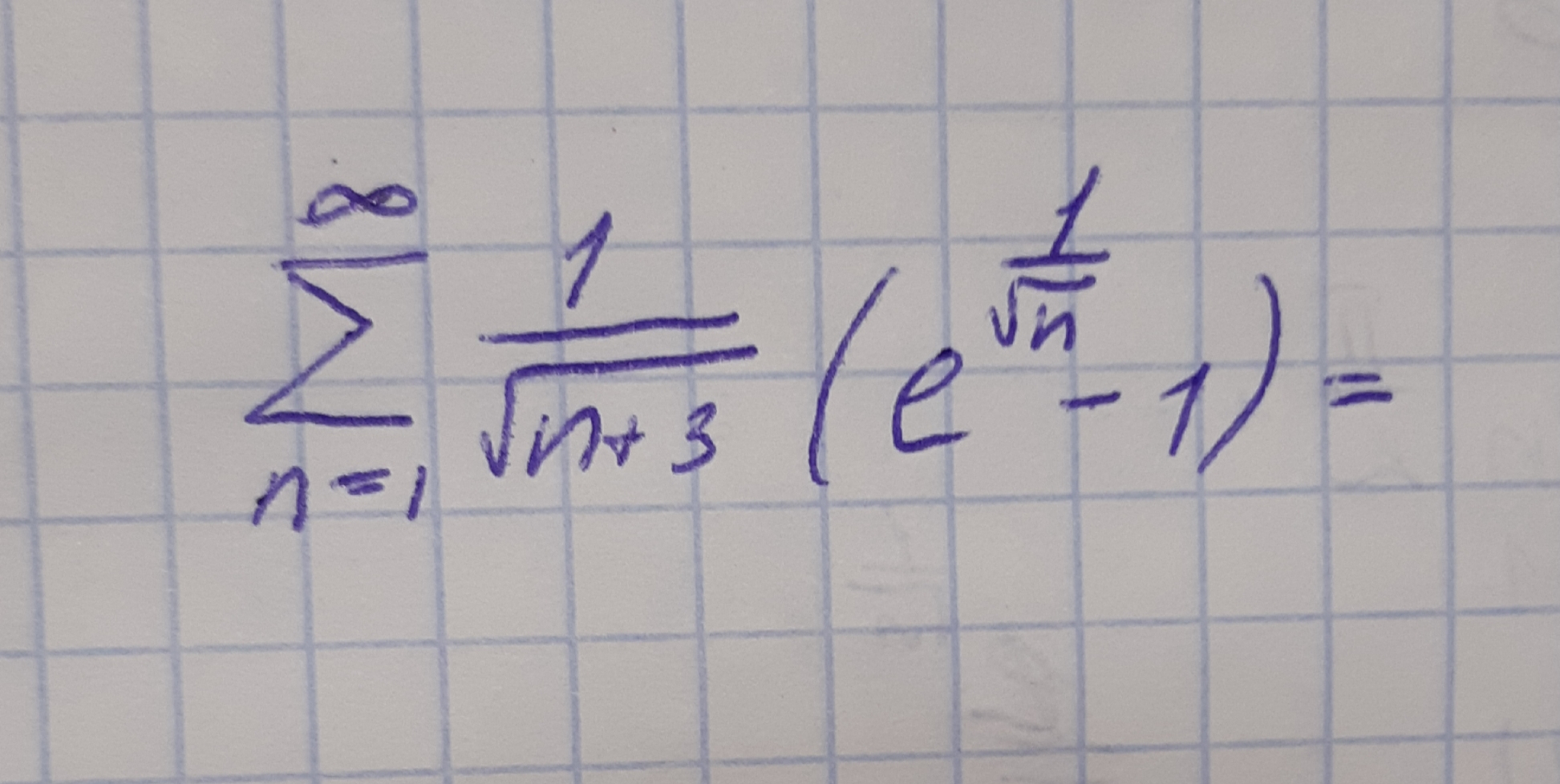
Решение
При n=1
a_(1)=[m]\frac{1}{\sqrt[4]{1^3}}sin\frac{\pi}{6}=\frac{1}{2}[/m].
При n=2
a_(2)=[m]\frac{1}{\sqrt[4]{2^3}}sin\frac{3\pi}{6}=\frac{1}{\sqrt[4]{8}}[/m].
При n=3
a_(3)=[m]\frac{1}{\sqrt[4]{3^3}}sin\frac{\pi}{6}=\frac{1}{2\sqrt[4]{27}}[/m].
При n=4
a_(4)=[m]\frac{1}{\sqrt[4]{4^3}}sin\frac{3\pi}{6}=\frac{1}{\sqrt[4]{64}}=\frac{1}{4}[/m].
[m]\sum_{2}^{\infty}\frac{1}{\sqrt[4]{n}}sin\frac{(2+(-1)^{n})\pi }{6}=\frac{1}{2}+\frac{1}{\sqrt[4]{8}}+\frac{1}{2\sqrt[4]{27}}+\frac{1}{4}+...[/m]
перегруппируем:
[m](\frac{1}{2}+\frac{1}{2\sqrt[4]{27}}+...) + (\frac{1}{\sqrt[4]{8}}+\frac{1}{4}+...)=[/m]
[m]\sum_{1}^{\infty}\frac{1}{\sqrt[4]{(2k-1)^3}}sin\frac{\pi }{6}+\sum_{1}^{\infty}\frac{1}{\sqrt[4]{(2k)^3}}sin\frac{\pi }{2}=[/m]
[m]=\sum_{1}^{\infty}\frac{1}{\sqrt[4]{(2k-1)^3}}\cdot\frac{1 }{2}+\sum_{1}^{\infty}\frac{1}{\sqrt[4]{(2k)^3}}\cdot 1=[/m]
[m]=\sum_{1}^{\infty}\frac{1}{\sqrt[4]{2\cdot(2k-1)^3}}+\sum_{1}^{\infty}\frac{1}{\sqrt[4]{(2k)^3}}[/m]
Ряд
[m]\sum_{1}^{\infty}\frac{1}{\sqrt[4]{m^3}}=\sum_{1}^{\infty}\frac{1}{m^{\frac{3}{4}}}[/m]- расходится, так как
[m]\frac{3}{4} <1[/m]
Значит и данный ряд расходится как сумма двух расходящихся знакоположительных рядов. (+ ∞ + ∞ )=+ ∞
2.
[m]\sum^{\infty}_{1} \frac{1}{\sqrt{n+3}}(e^{\frac{1}{\sqrt{n}}}-1)=\sum^{\infty}_{1} \frac{1}{\sqrt{n+3}}\frac{1}{\sqrt{n}}\frac{(e^{\frac{1}{\sqrt{n}}}-1)}{\frac{1}{\sqrt{n}}}[/m]
Так как
[m]\lim_{n \to \infty}\frac{(e^{\frac{1}{\sqrt{n}}}-1)}{\frac{1}{\sqrt{n}}}=1[/m]
данный ряд эквивалентен ряду
[m]\sum^{\infty}_{1} \frac{1}{\sqrt{n+3}}\frac{1}{\sqrt{n}}=\sum^{\infty}_{1} \frac{1}{\sqrt{(n+3)n}}[/m]
Так как
[m]\lim_{n \to \infty}\frac{1}{\sqrt{(n+3)n}}:\frac{1}{n}=1[/m]
и ряд
[m]\sum^{\infty}_{1} \frac{1}{n}[/m] - расходится ( это гармонический ряд), то и данный ряд расходится.