Задача 41443 Даны две вершины треугольника ABC: A(-6...
Условие
Все решения
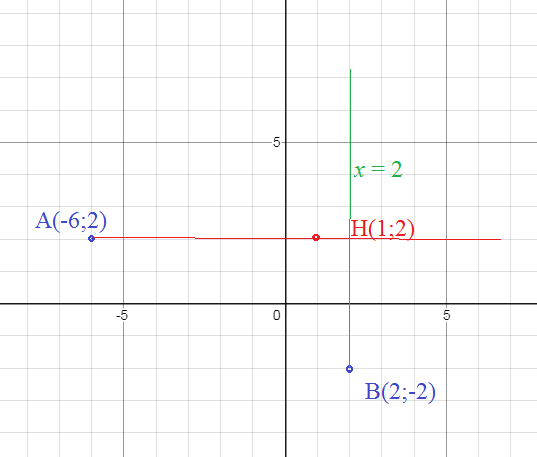
Уравнение прямой АН:
y=2
Значит уравнение стороны BC:
x=2
Уравнение прямой АВ, как прямой, проходящей через две данные точки имеет вид:
(x-x_(A))/(x_(B)-x_(A))=(y-y_(A))/(y_(B)-y_(A))
Подставляем координаты точек
A(–6 ,2) и В(2, –2)
(x+6)/(2+6)=(y-2)/(-2-2)
-x-6=2y-4
[b]х+2у+2=0[/b] - уравнение АВ
y=-(1/2)x-1
k=-1/2
Угловой коэффициент перпендикулярной ей прямой k=2
Прямая СH имеет вид:
y=2x+b
Чтобы найти b подставим координаты точки Н
2=2*1+b
b=0
y=2x - уравнение высоты СН
Значит, СН и ВН пересекаются в точке С(2;4)
Составим уравнение прямой АС, как прямой проходящей через две точки А и С:
(x+6)/(2+6)=(y-2)/(4-2)
(х+6)/8=(у-2)/2
(х+6)/4=у-2
[b]x-4y+14=0 [/b] - уравнение АС
Уравнение ВН, как прямой проходящей через две точки В и Н:
(x-2)/(1-2)=(y+2)/(2+2)
[b]4х+y-6=0[/b] - уравнение ВН
Находим точку пересечения АС и BH
{x-4y+14=0 ⇒ x=4y-14
{4х+y-6=0
4*(4y-14)+y-6=0
17y=62
y=62/17
x=4*(62/17)-14
считаем самостоятельно