Задача 414 В прямоугольном параллелепипеде...

slava191

11.01.2014

В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1=5, CC1=3, B1C1=sqrt(7).Найдите длину ребра AB.

Ответ: 3

vk397114329

19.05.2018

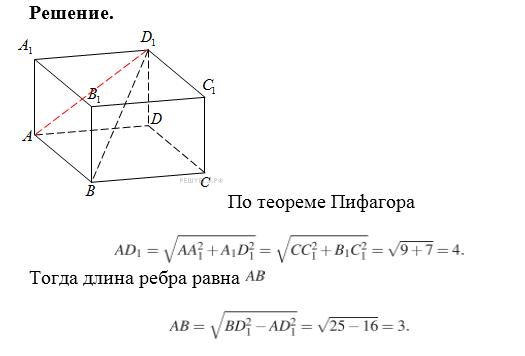
Решение:
В прямоугольном параллелепипеде AB^2+BC^2+BB1^2=BD1^2
Подставляя известные величины получаем
AB^2+BC^2+BB1^2=BD1^2
AB^2=25-7-9
AB^2=9 .
AB=3