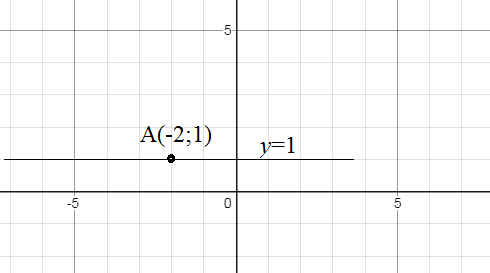Задача 41373 1) Составить уравнение прямой L...
Условие
y=1 ; x=-2 ; 2x-y=0
2) Составить уравнение прямой L проходящей через начало координат и точку A (-3;5).
-3y+5x=0 ; 3x-5y=0 ; 5x+3y=0
3) Указать угловой коэффициент и начальную ординату прямой 2k-3y+6=0.
k=2 d=6 ; k=2/3 b=-3 ; k=3/2 b=-3
4) Составить уравнение прямой L, которая наклонена к положительно направленной оси OX под углом в 45 градусов и имеющей начальную ординату b=-3.
y-x+3=0 ; x+y+3=0 ; x-y+3=0
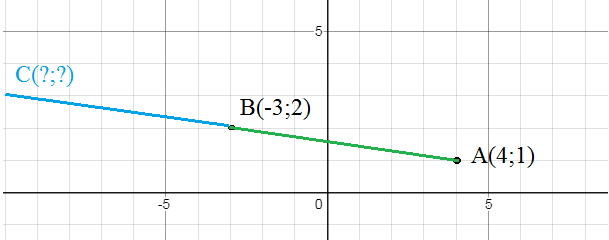
5) Отрезок AB продолжен за точкой B и удлинен в 2 раза до точки С. Причем A (4;1), B (-3;2). Составить уравнени
..
Решение
О т в е т.[b]y=1[/b] ( cм. рис.1)
2)
y=kx - общий вид прямых, проходящих через начало координат
Подставим координаты точки А(-3;5): х=-3; у=5
5=k*(-3)
k=[m]\frac{-5}{3}[/m]
y=[m]\frac{-5}{3}[/m]x ⇒ 3y=-5x;
[b]3y+5x=0 [/b]
О т в е т.[b]3y+5x=0 [/b]
3)
2х-3у+6=0 ⇒
находим 3у:
3у = 2х+6 ( делим на 3)
y=[m]\frac{2}{3}x+2[/m] - уравнение прямой вида y=kx+b, значит
k=[m]\frac{2}{3}[/m]
b=2
4)
В общем уравнении прямой вида y=kx+b
угловой коэффициент k=tg α , где α - угол наклона прямой с положительным направлением оси Ох
Так как [i]по условию[/i] угол наклона прямой с положительным направлением оси Ох
α =45 °
и
tg 45 ° =1, значит k=1
[i]по условию[/i] b=-3
Подставляем в уравнение y=kx+b, получаем
[b]y=x-3[/b] ⇒ y-x+3=0
О т в е т. y-x+3=0
5)
Точка В - середина отрезка АС
x_(B)=[m]\frac{x_{A}+x_{C}}{2}[/m]
y_(B)=[m]\frac{y_{A}+y_{C}}{2}[/m]
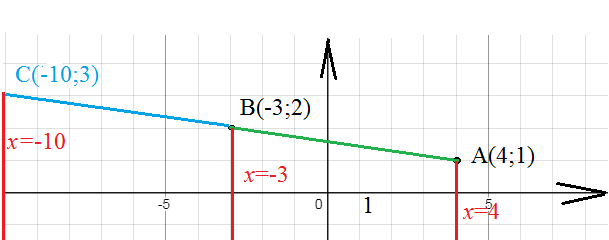
x_(C)=2x_(B)-x_(A)=2*(-3)-4=-10
y_(C)=2y_(B)-y_(A)=2*2-1=3
[red]C(-10;3)[/red]
Уравнение прямой, проходящей через точку С перпендикулярно оси Ох:
x=-10
или
[b]x + 10 = 0[/b]
Уравнение прямой, проходящей через точку B перпендикулярно оси Ох:
x=-3
или
[b]x + 3 = 0[/b]
Уравнение прямой, проходящей через точку A перпендикулярно оси Ох:
x=4
или
[b]x - 4 = 0[/b]