Задача 41365 ...

vk223840790

2019-11-09 12:30:10

sqrt(2x+8)+ sqrt(10 − 2x) ≥ log2 (4x^2 - 4x + 65)
Поставлю свечку за того кто решит)))

sova

2019-11-09 12:57:08

★

ОДЗ:
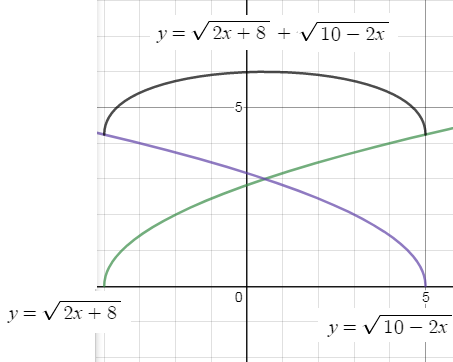
{2x+8 ≥ 0 ⇒ x ≥ -4
{10-2x ≥ 0 ⇒ x ≤ 5
{4x^2-4x+65 >0 - верно при любом х, так как D <0

ОДЗ: х ∈ [-4; 5]

y=4x^2-4x +65 принимает значения от 64 до + ∞
Значит
log_(2)(4x^2-4x+65) ≥ log_(2)(64)=6

y=sqrt(2x+8)+sqrt(10-2x) принимает на [-4;5] значения
меньше или равные 6 ( см. рис)

Значит, неравенство верно, только как равенство, т.е при
sqrt(2x+8)+sqrt(10-2x) =6
или
log_(2)(4x^2-4x+65)=6 ⇒ 4x^2-4x+65=2^6 ⇒ 4x^2-4x+1=0 ⇒ (2x-1)^2=0 ⇒ 2x-1=0 ⇒ x=0,5

0,5 ∈ ОДЗ

О т в е т. 0,5