Задача 41354 ...
Условие
B = {2, 7, 12, 14, 35}
C = {3, 7, 21, 24, 14, 11}
a) (A ∩ B) ∩ (B ∪ C)
b) A ∪ B ∪ C
c) (B \ A) ∪ (C \ A)
2) a) (A ∪ B) \ (C ∩ A)
b) A ∪ B ∪ C
c) B ∩ (A ∩ C)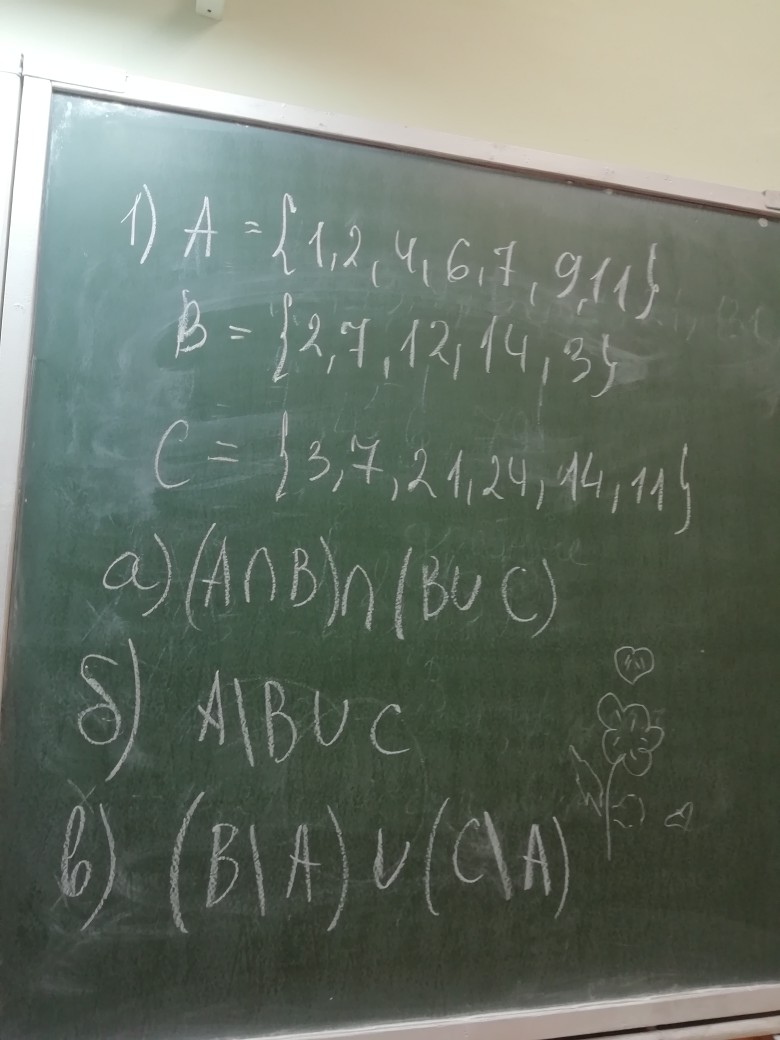
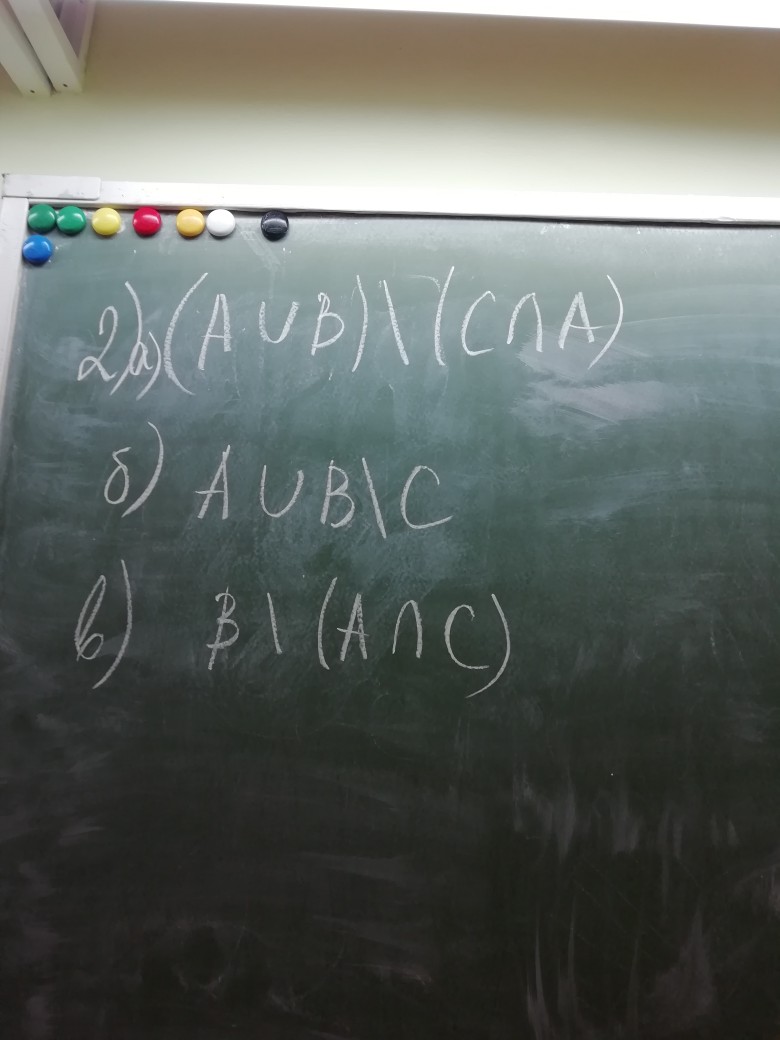
математика ВУЗ
577
Решение
★
а)
A ∩ B={2,7}
B ∪ C={2,3,7,11,12,14,21,24}
(A ∩ B) ∩(B ∪ C)={2,7}
б)
A\B={1,4,6,9}
(A\B) ∪ C={1,3,4,6,7,9,11,21,24}
в)
B\A={3,12,14}
C\A={3,14,21,24}
(B\A)U(C\A)={3,12,14,21,24}
2
a)
A ∪ B={1,2,3,4,6,7,9,11,12,14}
C ∩ A={3,7}
(A ∪ B)\(C ∩ A)={1,2,4,6,9,11,12,14}
б)
A ∪ B={1,2,3,4,6,7,9,11,12,14}
(A U B)\C={1,2,4,6,9,12,14}
в)
A ∩ C={3,7}
B\(A ∩ C)={2,12,14}
