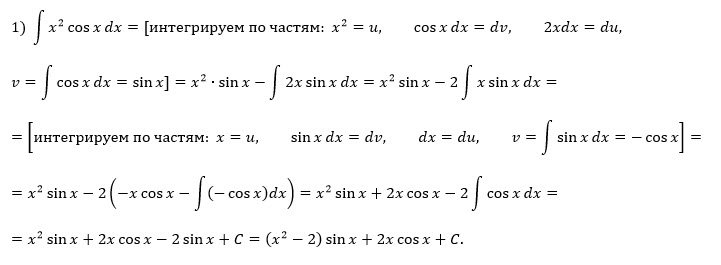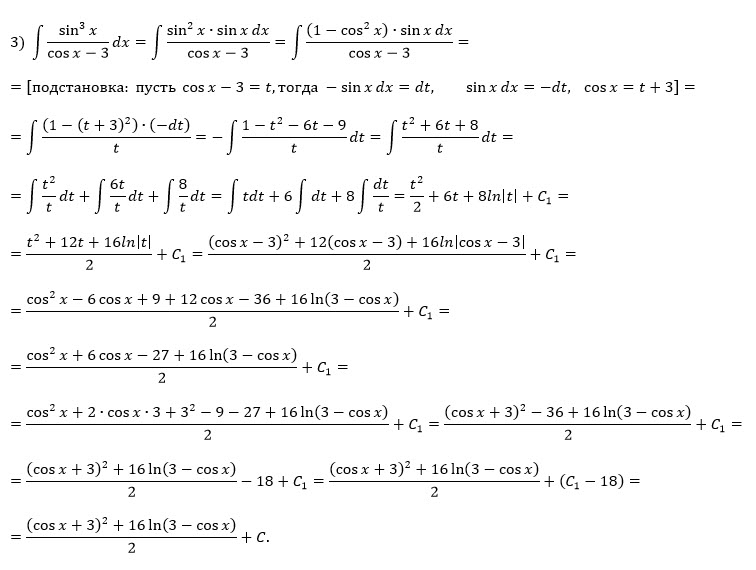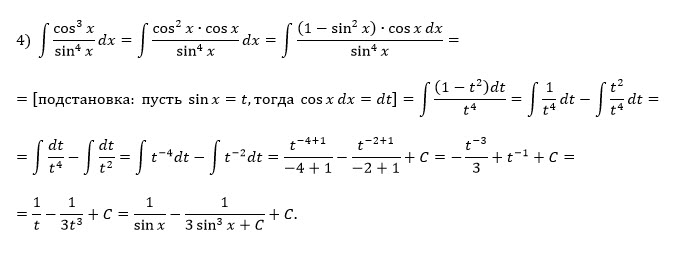Задача 41327 Пожалуйста помогите найти интеграл...
Условие
Интеграл x^2cosx dx
Интеграл dx/sin x
Интеграл sin^3 x / cosx -3 dx
Интеграл cos^3 x / sin^4 x
Все решения
[blue] ∫ x^2cosxdx[/blue]
по частям:
u=x^2
dv=cosxdx
du=2xdx
v=sinx
[blue]∫ x^2cosxdx=x^2*sinx- ∫ sinx*(2x)dx=x^2*sinx-2∫ x*sinxdx=[/blue]
еще раз по частям:
u=x
dv=sinxdx
du=dx
v=-cosx
[blue]=x^2*sinx-2*(x*(-cosx) - ∫ (-cosx)dx)=[/blue]
[blue]=x^2*sinx +2xcosx-2 ∫cosxdx=[/blue]
=[blue]x^2sinx+2xcosx-2sinx + C[/blue]
2.
[m]\int \frac{dx}{sinx}=\int \frac{sin^2\frac{x}{2}+cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}dx=\int \frac{sin^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}dx+\int \frac{cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}dx=[/m]
[m]=\int \frac{sin\frac{x}{2}}{2cos\frac{x}{2}}dx+\int \frac{cos\frac{x}{2}}{2sin\frac{x}{2}}dx=[/m]
[m]=-ln|cos\frac{x}{2}|+ln|sin\frac{x}{2}|+C=ln|tg\frac{x}{2}|+C[/m]
3.
Замена
cosx-3=t
cosx=t+3
d(cosx)=d(t+3)
-sinxdx=dt ⇒[red] sinxdx=-dt[/red]
cos^2x=(t+3)^2
sin^2x=1-cos^2x=1-(t+3)^2=(1-t-3)(1+t+3)=(t+4)*(-t-2)=
=-(t+4)(t+2)=-(t^2+6t+8)
[m]\int \frac{sin^3x}{cosx-3}dx=\int \frac{sinx\cdot sin^2x}{cosx-3}dx=\int \frac{t^2+6t+8}{t}dt=[/m]
= ∫ (t+6+[m]\frac{8}{t}[/m])dt=
=[m]\frac{t^2}{2}[/m]+6t+8ln|t|+C=
обратный переход:
=[m]\frac{(cosx-3)^2}{2}[/m]+6*(cosx-3)+8ln|cosx-3|+C
4.
[m]\int \frac{cos^3x}{sin^4x}dx=\int \frac{cosx\cdot cos^2x}{sin^4x}dx=[/m]
[m]=\int \frac{cosx\cdot (1-sin^2x)}{sin^4x}dx=[/m]
[m]=\int \frac{1}{sin^4x}cosdx-\int \frac{sin^2x}{sin^4x}(cosxdx)=[/m]
[m]=\int \frac{d(sinx)}{sin^4x}-\int \frac{d(sinx)}{sin^2x}=[/m]
[m]=\int \frac{dt}{t^4}-\int \frac{du}{u^2}=[/m]
[m]=-\frac{1}{3sin^3x}+\frac{1}{sinx} + C[/m]