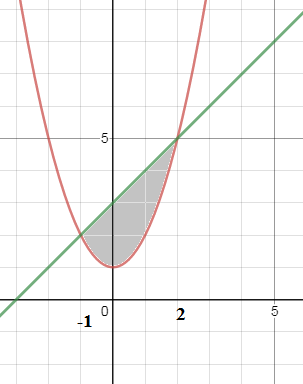
Задача 41268 Найти площадь фигуры, ограниченной...

vk492803606

6 ноября 2019 г. в 17:20

Найти площадь фигуры, ограниченной линиями y = x² + 1 и y = x + 3.

sova

6 ноября 2019 г. в 17:23

★

Найдем абсциссы точек пересечения графиков:
x²+1=x+3
x²–x–2=0
D=1+8=9
x₁=–1; x₂=2

S= ∫ ²_–1(x+3–(x²+1))dx= ∫ ²_–1(x+2–x²)dx=

[m]=(\frac{x^2}{2}-\frac{x^3}{3}+2x)|^{2}_{-1}=[/m]

[m]=\frac{2^2}{2}-\frac{2^3}{3}+2\cdot 2 - (\frac{(-1)^2}{2}-\frac{(-1)^3}{3}+2\cdot (-1) =4,5[/m]