Задача 40980 Выполнить действия с комплексными...
Условие
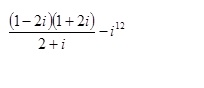
математика ВУЗ
743
Решение
★
[m]=\frac{5-2-i}{2+i}=\frac{3-i}{2+i}=[/m]
[m]\frac{(3-i)(2-i)}{(2+i)(2-i)}=\frac{6-2i-3i+i^2}{4-i^2}=\frac{6-5i-1}{5}=\frac{5-5i}{5}=1-i[/m]
|1-i|=sqrt(1^2+(-1)^2)=sqrt(2)
[m]arg(1-i)=\frac{-\pi}{4}[/m]
[m]1-i=\sqrt{2}\cdot (cos(\frac{-\pi}{4})+isin(\frac{-\pi}{4}))=
\sqrt{2}(cos(\frac{\pi}{4})-sin(\frac{\pi}{4}))[/m] - в тригонометрической
[m]1-i=\sqrt{2}\cdot e^{\frac{-\pi}{4}i}[/m]- в показательной