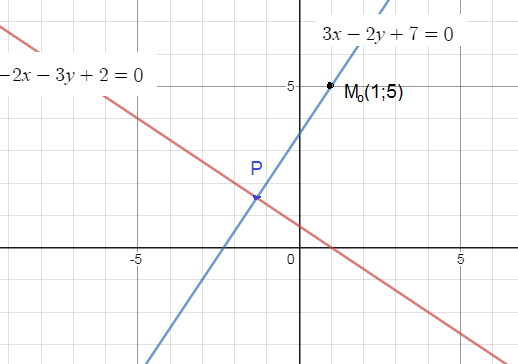
Задача 40928 Напишите общее уравнение прямой,...

clubmix_

2019-10-24 11:32:42

Напишите общее уравнение прямой, проходящей через точку M0(1;5) перпендикулярно прямой −2x−3y+2=0. Определите угловой коэффициент k и отрезок b, отсекаемый на оси Oy прямой, уравнение которой Вы записали. Найдите точку P(x;y) пересечения прямых.

sova

2019-10-24 15:47:27

[i]l[/i]_(1):
-2х-3у+2=0 ⇒ y=[m]-\frac{2}{3}x+\frac{2}{3}[/m]
k_(1)=[m]-\frac{2}{3}[/m]

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k_(1)*k_(2)=-1

k_(2)=[m]-\frac{1}{k_{1}}=-\frac{1}{-\frac{2}{3}}=\frac{3}{2}=1,5[/m]-угловой коэффициент искомой прямой

Значит уравнение искомой прямой принимает вид:
y=1,5x+b

Чтобы найти b подставляем координаты точки M_(o):

5=1,5*1+b

b=5-1,5=3,5- отрезок, отсекаемый на оси Оу

y=1,5x+3,5 - уравнение искомой прямой с угловым коэффициентом.
Умножаем на 2:
2y=3x+7 ⇒ [blue]3x-2y+7=0 - общее уравнение искомой прямой
[/blue]
Чтобы найти точку пересечения прямых решим систему:
{-2x-3y+2=0
{y=1,5x+3,5

Подставляем у из второго уравнения в первое:

-2х-3*(1,5x+3,5)+2=0

-2x-4,5-10,5+2=0

-6,5x=8,5

x=[m]-\frac{85}{65}=-\frac{17}{13}[/m]

y=1,5*([m]-\frac{17}{13}[/m])+3,5

y=([m]\frac{15}{10}\cdot (-\frac{17}{13})+\frac{35}{10}[/m]

y=[m]\frac{15\cdot (-17)+35\cdot 13}{130}=\frac{20}{13}[/m]

P([m]-\frac{17}{13}; \frac{20}{13})[/m]

О т в е т.
3х-2y+7=0
k=1,5
b=3,5
P([m]-\frac{17}{13}; \frac{20}{13})[/m]