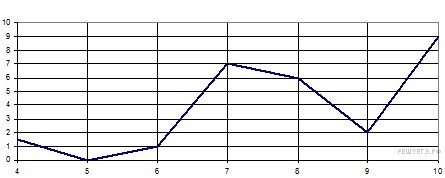
Задача 409 На рисунке изображен график осадков в г....
Условие
математика 10-11 класс
9069
Решение
Ответ: 3
Все решения
О т в е т. 3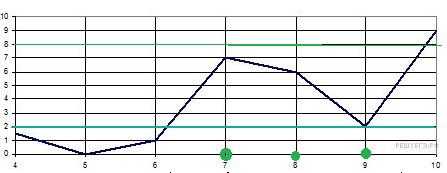

Ответ: 3
О т в е т. 3