Задача 40827 ...
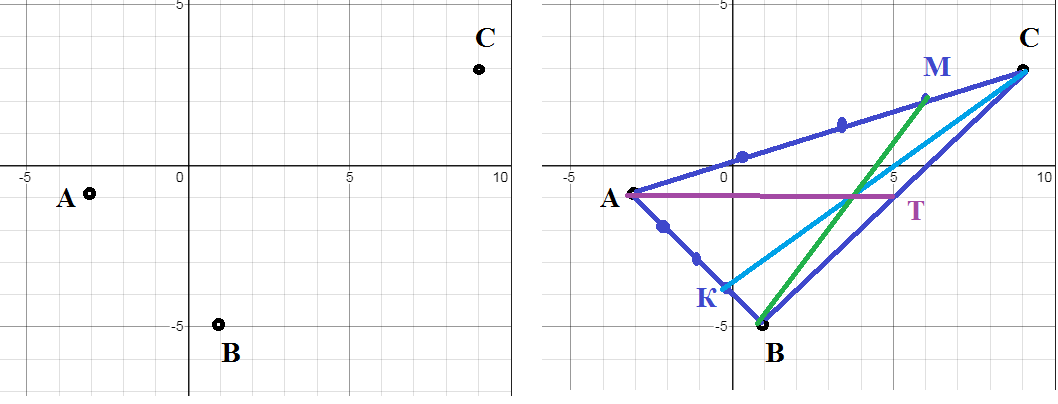
Условие
Решение
х_(К)=[m]\frac{-3+3*1}{1+3}=0[/m]
y_(К)=[m]\frac{-1+3*(-5)}{1+3}=-4[/m]
Cоставляем уравнение прямой СК:
=[m]\frac{x-0}{9-0}=\frac{y-(-4)}{3-(-4)}[/m]
[blue]7x-9y=36[/blue]
Аналогично
По формулам деления отрезка в данном отношении находим координаты точки M
х_(M)=[m]\frac{-3+3*9}{1+3}=6[/m]
y_(M)=[m]\frac{-1+3*3}{1+3}=2[/m]
Cоставляем уравнение прямой BM:
=[m]\frac{x-6}{1-6}=\frac{y-2}{-5-2}[/m]
-7(x-6)=-5(y-2)
[blue]7х-5y=32[/blue]
Аналогично
По формулам деления отрезка пополам находим координаты точки Т
х_(T)=[m]\frac{1+9}{2}=5[/m]
y_(T)=[m]\frac{-5+3}{2}=-1[/m]
Cоставляем уравнение медианы AT:
[blue]y=-1[/blue]
{7x-9y=36
{7x-5y=32
{y=-1
7x+9=36
7x+5=32
([m]\frac{27}{7}[/m];1) - единственная точка принадлежащая всем трем уравнениям