Задача 40802 доказать,что векторы образуют базис...
Условие
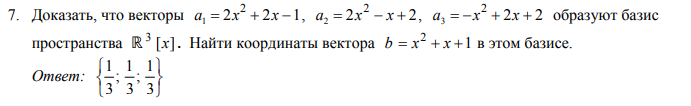
Решение
Чтобы доказать,что векторы a_(1);a_(2);a_(3) образуют базис, достаточно показать, что они линейно независимы.
Составляем их линейную комбинацию
α_(1)[b]a_(1)[/b]+ α_(2)[b]a_(2)[/b]+ α_(3)[b]a_(3)[/b]=
= α_(1)(2x^2+2x-1)+α_(2)(2x^2-x+2)+α_(3)(-x^2+2x+2)=
=(2α_(1)+2α_(2)-α_(3))*x^2+(2α_(1)-α_(2)+2α_(3))*x+(-α_(1)+2α_(2)+2α_(3))
(2α_(1)+2α_(2)-α_(3))*x^2+(2α_(1)-α_(2)+2α_(3))*x+(-α_(1)+2α_(2)+2α_(3))=0 ⇒
{2α_(1)+2α_(2)-α_(3)=0
{2α_(1)-α_(2)+2α_(3)=0
{-α_(1)+2α_(2)+2α_(3)=0
[m]\Delta =\begin{vmatrix} 2 & 2 &-1 \\ 2 &-1 & 2\\ -1 &2 & 2 \end{vmatrix}=-4-4-4+1-8-8\neq 0[/m]
Система имеет единственное нулевое решение
α_(1)=α_(2)=α_(3)=0
Значит векторы линейно независимы и образуют базис
b= β _(1)[b]a_(1)[/b]+ β _(2)[b]a_(2)[/b]+ β _(3)[b]a_(3)[/b]=
=(2 β β _(1)+2 β _(2)- β _(3))*x^2+(2 β _(1)- β _(2)+2 β _(3))*x+(- β _(1)+2 β _(2)+2 β _(3))
По условию
b=x^2+x+1
{2 β _(1)+2 β _(2)- β _(3)=1
{2 β _(1)- β _(2)+2 β _(3)=1
{- β _(1)+2 β _(2)+2 β _(3)=1
Решаем систему методом Крамера
[m]\Delta =\begin{vmatrix} 2 & 2 &-1 \\ 2 &-1 & 2\\- 1 &2 & 2 \end{vmatrix}=-4-4-4+1-8-8=-27[/m]
[m]\Delta_{1}=\begin{vmatrix} 1 & 2 &-1 \\ 1 &-1 & 2\\ 1 &2 & 2 \end{vmatrix}=-2+4-2-1-4-4=-9[/m]
[m]\Delta_{2} =\begin{vmatrix} 2 & 1 &-1 \\ 2 &1 & 2\\ -1 &1 & 2 \end{vmatrix}=4-2-2-1-4-4=-9[/m]
[m]\Delta_{3} =\begin{vmatrix} 2 & 2 &1 \\ 2 &-1 & 1\\ -1 &2 & 1 \end{vmatrix}=-2-2+4-1-1-4=-9[/m]
[m]\beta_{2}=\frac{\Delta_{2}}{\Delta}=\frac{-9}{-27}=\frac{1}{3}[/m]
[m]\beta_{3}=\frac{\Delta_{3}}{\Delta}=\frac{-9}{-27}=\frac{1}{3}[/m]
[m]\beta_{1}=\frac{\Delta_{1}}{\Delta}=\frac{-9}{-27}=\frac{1}{3}[/m]
О т в е т. {[m]\frac{1}{3},\frac{1}{3},\frac{1}{3}[/m]}
