Задача 4078 Центр окружности, описанной около...

Anton

15.10.2015

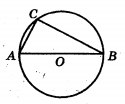
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48.

Угол ACB - вписан в окружность. Величина вписанного угла [b]в два раза меньше[/b] гр.адусной меры дуги, на которую он опирается. Градусная мера круга 360 градусов. Дуга AB - половина круга, значит ее градусная мера 360/2 = 180 градусов. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 градусов.

AB = 2R = 2*25 = 50
По т. Пифагора найдём AC
AC^2 = AB^2-CB^2
AC = sqrt(AB^2-CB^2)
AC = sqrt(50^2-48^2)
AC = sqrt(196) = 14


Ответ: 14