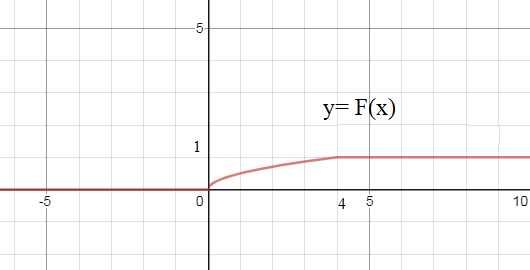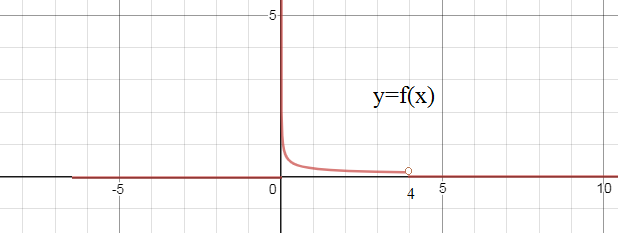Задача 40769 ...

leronmarkevich

20 октября 2019 г. в 19:40

Непрерывная случайная величина задана функцией распределения F(x). Найти плотность вероятности f(x). Построить графики функций F(x) и f(x). Найти вероятность события (X ∈ [a; b]). Воспользуйтесь следующими данными:

[m]
F(x) =
\begin{cases}
0, & x < 0; \\
\frac{1}{2} \sqrt{x}, & 0 \leq x < 4; \quad a = 1, \quad b = 4. \\
1, & x \geq 4. \\
\end{cases}
[/m]

sova

20 октября 2019 г. в 21:03

★

f(x)=F`(x)
поэтому

[m]f(x)=\begin{cases} &0, x<0 \\ & \frac{1}{2}\cdot {(\sqrt{x})}', 0\leq x<4 \\ &0 , x\geq 4 \end{cases}[/m]

[m]f(x)=\begin{cases} &0, x<0 \\ & \frac{1}{2}\cdot {(x^{\frac{1}{2}})}', 0\leq x<4 \\ &0 , x\geq 4 \end{cases}[/m]

[m]f(x)=\begin{cases} &0, x<0 \\ & \frac{1}{4\sqrt{x}}, 0\leq x<4 \\ &0 , x\geq 4 \end{cases}[/m]

Графики см. рис.

[m]P(1\leq X\leq 4)=F(4)-F(1)=\frac{1}{2}\sqrt{4}-\frac{1}{2}\sqrt{1}=1-\frac{1}{2}=\frac{1}{2}[/m]