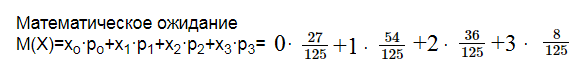Задача 40768 В урне - очень большое количество черных...

leronmarkevich

20 октября 2019 г. в 19:34

В урне – очень большое количество черных и белых шаров в пропорции 2:3. Извлекают 3 шарика. Случайная величина – количество черных шариков среди извлеченных. Решив задачу, для этой величины записать закон распределения и найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

sova

20 октября 2019 г. в 21:33

★

Среди трех извлеченных шариков может быть 0 черных, или 1 черный, или 2 черных или 3 черных

Это и есть значения случайной величины.

Теперь считаем их вероятности.
Вероятность вынуть белый шар равна [m]\frac{3}{5}[/m]
Вероятность вынуть черный шар равна [m]\frac{2}{5}[/m]

При Х=0
все три шарика белые.
Вероятность вынуть белый шар равна [m]\frac{3}{5}[/m]
Вероятность того, что все три шара белые:
p_o=[m]\frac{3}{5}\cdot \frac{3}{5}\cdot \frac{3}{5}=\frac{27}{125} [/m]

При Х=1
Вероятность того, что один шар черный, два белых
p₁=C¹₃[m]\frac{2}{5}\cdot (\frac{3}{5})^{2}=\frac{54}{125}[/m]

При Х=2
Вероятность того, что два шара черных, один белый
p₂=C²₃[m](\frac{2}{5})^{2}\cdot \frac{3}{5}=\frac{36}{125}[/m]

При X=3
Вероятность того, что все три шара черные:
p₃=[m]\frac{2}{5}\cdot \frac{2}{5}\cdot \frac{2}{5}=\frac{8}{125} [/m]

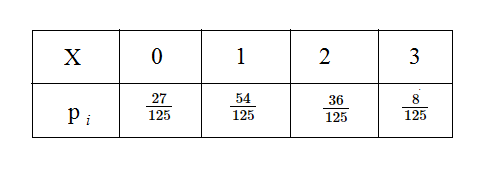
Таблица ( и есть закон распределения)