Задача 40744 Решить показательное уравнение...
Условие
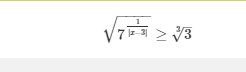
Все решения
[m]\sqrt{7^{\frac{1}{|x-3|}}}=(7^{\frac{1}{|x-3|}})^{\frac{1}{2}}=7^{\frac{1}{2\cdot |x-3|}}[/m]
∛3=[m]3^{\frac{1}{3}}[/m]
Логарифмируем по основанию 3
Логарифмическая функция с основанием 3 возрастает, поэтому знак неравенства сохраняется:
[m]log_{3}7^{\frac{1}{2\cdot |x-3|}}\geq log_{3}3^{\frac{1}{3}}[/m]
По свойству логарифма степени:
[m]\frac{1}{2\cdot |x-3|}\cdot log_{3}7\geq\frac{1}{3}[/m]
[m]\frac{1}{2\cdot |x-3|}\geq\frac{1}{3log_{3}7}[/m]
2|x-3| ≤ 3log_(3)7 ( свойства неравенств)
[m]|x-3|\leq \frac{3log_{3}7}{2}[/m]
[m]-\frac{3log_{3}7}{2}\leq x-3\leq\frac{3log_{3}7}{2}[/m]
Прибавить 3:
[m]3 -\frac{3log_{3}7}{2}\leq x\leq3+\frac{3log_{3}7}{2}[/m]
x ≠ 3
О т в е т. [m](3 -\frac{3log_{3}7}{2}; 3) U (3;3+\frac{3log_{3}7}{2})=[/m]
=[m](3 -\frac{3}{2}\cdot log_{3}7; 3) U (3;3+\frac{3}{2}\cdot log_{3}7)=[/m]
[m]=(3 -log_{3}7^{\frac{3}{2}}; 3) U (3;3+log_{3}7^{\frac{3}{2}})=[/m]
[m]=(3 -log_{3}\sqrt{343}; 3) U (3;3+log_{3}\sqrt{343})[/m]