Задача 40717 Найдите все значения параметра а при...

nikolay179540

2019-10-18 16:52:56

Найдите все значения параметра а при которых уравнение x^2-2(a-2)x+a^2-2a-3 = 0 имеет два различных положительных корня

sova

2019-10-18 18:10:40

Корни есть и они различные, значит D >0

D=(2(a-2))^2-4*(a^2-2a-3)=4a^2-16a+16-4a^2+8a+12=28-8a

28-8a >0

a< [m]\frac{7}{2}[/m]

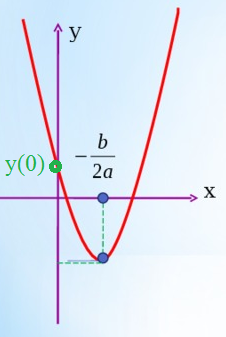
Корни положительные, значит парабола y=x^2-2(a-2)x+a^2-2a-3
пересекает ось Ох справа от нуля.

Значит вершина параболы правее нуля, т.е
x_(o)=a-2
x_(o) >0

a-2 >0

Значение функции y=x^2-2(a-2)x+a^2-2a-3 при х=0 положительно.
y(0)=a^2-2a-3

Система:
{a< [m]\frac{7}{2}[/m]
{a-2 > 0 ⇒ a > 2
{a^2-2a-3 >0 ⇒ D=16; корни -1 и 3, a<-1 или a>3


О т в е т. (3;3,5)