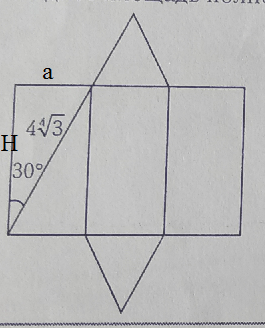
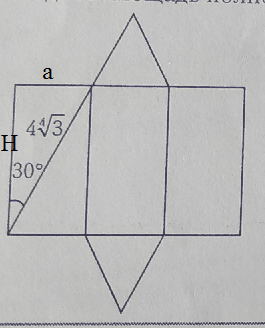
Задача 40714 На рисунке изображена развертка...
Условие
математика 10-11 класс
9169
Все решения
равен половине гипотенузы.
Значит легко найти
a=[m]2\sqrt[4]{3}[/m]
H=[m]4\sqrt[4]{3}cos 30^{o}=2\sqrt[4]{3}\sqrt{3}[/m]
S_(осн)=[m]a^2\frac{\sqrt{3}}{4}=3[/m]
S_(бок)=3a*H=3*[m]2\sqrt[4]{3}[/m]*[m]2\sqrt[4]{3}\sqrt{3}[/m]=36
S_(полн)=S_(бок)+2S_(осн)=36+6=[b]42[/b]