Задача 40687 ...
Условие
Найдите скалярное → →
произведение BC*CD 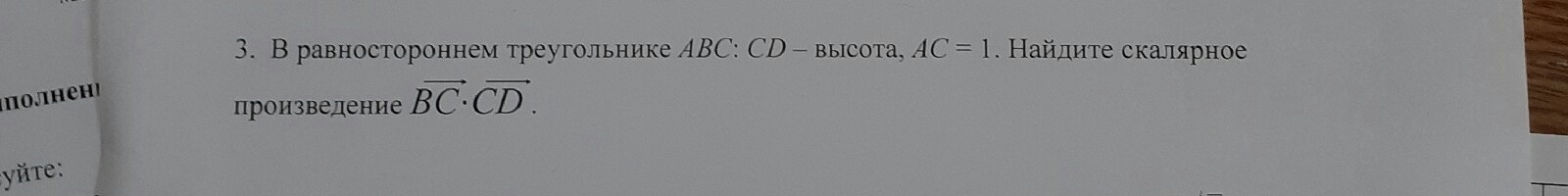
Решение
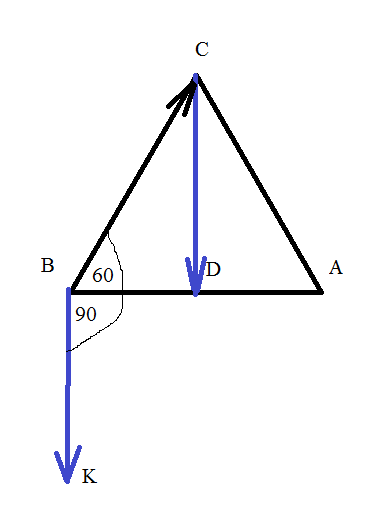
Высота СD является и медианой, значит BD=DA=[m]\frac{1}{2}[/m]
и биссектрисой, значит ∠ BCD= ∠ ACD=30 °
По определению скалярное произведение векторов, [i]выходящих [/i] из одной точки равно произведению[i] длин[/i] этих векторов на [i]косинус[/i] угла между ними.
Перенесем начало вектора vector{CD} в точку B.
vector{BK}=vector{CD}
|vector{BK}|=|vector{CD}|=[m]\frac{\sqrt{3}}{2}[/m]
Тогда угол между векторами vector{BC} и vector{BK} равен 150 °
cos150 ° =cos(180 ° - 30 °) =-cos30 ° =[m]-\frac{\sqrt{3}}{2}[/m]
vector{BС}*vector{СD}=vector{BС}*vector{BK}=|BC|*|BK|*cos150 ° =[m]1\cdot \frac{\sqrt{3}}{2}\cdot (-\frac{\sqrt{3}}{2})=-\frac{3}{4}[/m]