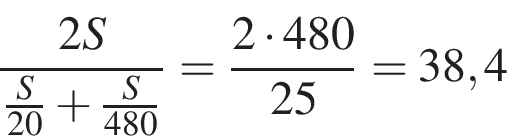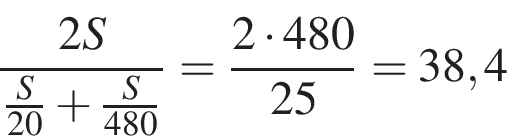Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
математика 10-11 класс
55762
Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть 2S км — весь путь путешественника, тогда средняя скорость равна:
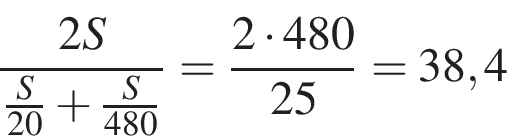
Ответ: 38.4
Вопросы к решению (1)
Чтобы сложить дроби S/20 и S/480 нам надо привести их к общему знаменателю. Для этого дробь S/20 надо записать в виде 24S/480, теперь можно сложить 24S/480+S/480 = 25S/480. Дальше дробь переворачивает, и S сокращается - так и получается 25 внизу