Задача 4024 Грузы массами М = 1 кг и m связаны...

slava191

14 октября 2015 г.

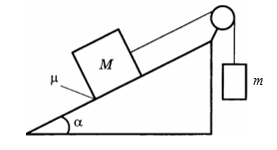
Грузы массами М = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?

Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости.

Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат.

На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:

Mg sin а – Т1 – Fтр = 0 (ось направлена вниз вдоль наклонной плоскости);

N – Mg cos а = 0 (ось направлена вверх перпендикулярно наклонной плоскости).

На второе тело действуют сила тяжести и сила натяжения нити: mg – Т2 = 0 (ось направлена вертикально вниз).

Учтем, что Т1 = Т2 = Т (нить легкая, между блоком и нитью трения нет), Fтр ≤ μN (сила трения покоя).

Получим:

mmin = М (sina – μcos а) 0,24 кг.

Ответ: mmln = М (sin а - μcosa) = 0,24 кг.