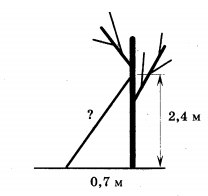
Задача 4009 Какова длина (в метрах) лестницы,...

Anton

13.10.2015

Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?

Воспользуемся теоремой Пифагора.
A^2 = B^2+C^2 A - длина лестницы.
A^2 = 0,7^2+2,4^2
A = sqrt(0,49+5.76)
A = sqrt(6,25)
A = 2,5


Ответ: 2,5