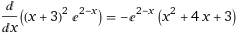Задача 39836 Найдите производную (x + 3)^2 * e^(2 -...
Условие
(x + 3)2 · e2 – x
предмет не задан
558
Решение
★
(u·v)`=u`·v+u·v`
((x+3)2·e2–x)`=[u=(x+3)2; v=e2–x]=
=((x+3)2)`·e2–x+(x+3)2·(e2–x)`=
применяем правило нахождения производной сложной функции
=2·(x+3)·(x+3)`·e2–x+(x+3)2·e2–x·(2–x)`=
=2·(x+3)·1·e2–x+(x+3)2·e2–x·(–1)=
=e2–x·(2x+6–x2–6x–9)=e2–x·(–x2–4x–3)
Обсуждения
Все решения
Обсуждения