Задача 39810 ...

vk301356398

23 сентября 2019 г. в 18:43

1) Решить уравнение X² + 4X + 16 = 0 Корни записать в показательной форме.
2) Вычислить, ответ дать в показательной форме e^–jn/3 / (–√3 + j)⁵
3) Найти частное 1 – √3j / (–2√3 + 2j)двуми способами:
а) в алгебраической форме
б) в тригонометрической форме
4) Найти все корни: 3√–64j

sova

23 сентября 2019 г. в 21:54

★

z²+4z+16=0
D=4²–4·16=16·(1–4)=–16·3
√D= ± 4√3i

z₁=(4–4√3i)/2=2–2sqrt·3)i; z₂=2+2√3i

|z₁|=|z₂|=√2²+( ± 2√3)²=√4+12=√16=4

argz₁= φ ₁
sin φ ₁=y₁/|z₁|=–2√3/4=–√3/2
cos φ ₁=x₁/|z₁|=2/4=1/2

φ ₁=–π/3

z₁=4·(cos(–π/3)+isin(–π/3)) – тригонометрическая форма записи
z₁=4·e^–i·(π/3) – показательная форма записи

argz₂= φ ₂
sin φ ₁=y₂/|z₂|=2√3/4=√3/2
cos φ ₂=x₂/|z₂|=2/4=1/2

φ ₂=π/3

z₂=4·(cos(π/3)+isin(π/3)) – тригонометрическая форма записи
z₂=4·e^i·(π/3) – показательная форма записи

О т в е т. 4·e^–i·(π/3);4·e^i·(π/3)

2.
z=– √3+i
|z|=√–√3²+1²=√4=2

argz= φ
sin φ =y/|z|=1/2
cos φ=х/|z|=–√3/2

φ =5π/6

z=2·(cos(5π/6) + i sin(5π/6))

z=2·e^i·(5π/6)


e^–i·(π/3)/2·e^i·(5π/6)=(1/2)·e^{i·(5π/6)–π/3}=(1/2)·e^i(π/2)

О т в е т.(1/2)·e^i(π/2)

3.
[m]\frac{1-i\sqrt{3}}{-2\sqrt{3}+2i}=\frac{i\sqrt{3}-1}{2\sqrt{3}-2i}=\frac{(i\sqrt{3}-1)(2\sqrt{3}+2i))}{(2\sqrt{3}-2i)(2\sqrt{3}+2i)}=[/m]

[m]=\frac{6i-2\sqrt{3}+2\sqrt{3}i^2-2i}{(2\sqrt{3})^{2}-(2i)^{2}}=\frac{-4\sqrt{3}+4i}{12+4}=\frac{-\sqrt{3}+i}{4}=-\frac{\sqrt{3}}{4}+i\frac{1}{4}[/m] – в алгебраической форме.

|z|=√(√3/4)²+(1/4)²=√(3/16)+(1/16)=√4/16=√1/4=1/2

argz= φ
sin φ =y/|z|=(1/4)/(1/2)=1/2
cos φ=х/|z|=(–√3/4)/(1/2)=–√3/2

φ =5π/6

z=(1/2)·(cos(5π/6) + i sin(5π/6)) – в тригонометрической форме

4.
z=64i
|z|=–64

argz= φ
sin φ =y/|z|=(–64)/(64)=–1
cos φ=х/|z|=0/(64)=0

φ =–π/2

z=64·(cos(–π/2)+isin(–π/2))
По формуле Муавра ( cм. приложение

∛(–64i)=4·(cos[m]\frac{\frac{-\pi}{2}+2πk}{3}+sin\frac{\frac{-\pi}{2}+2πk}{3})[/m]

k ∈ Z
При k=0
z₀=4·(cos[m](\frac{\frac{-\pi}{2}}{3})+sin(\frac{\frac{-\pi}{2}}{3}))=4\cdot (cos (\frac{-\pi}{6})+sin(\frac{-\pi}{6}))[/m]
При k=1
z₁=4·(cos[m](\frac{\frac{-\pi}{2}+2\pi}{3})+sin(\frac{\frac{-\pi}{2}+2pi}{3}))=4\cdot (cos (\frac{\pi}{2})+sin(\frac{\pi}{2}))[/m]
При k=2
z₂=4·(cos[m](\frac{\frac{-\pi}{2}+4\pi}{3})+sin(\frac{\frac{-\pi}{2}+4\pi}{3}))=4\cdot (cos (\frac{7\pi}{6})+sin(\frac{7\pi}{6}))[/m]

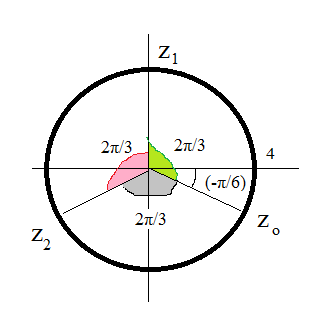
cм. рис.

три числа z_o;z₁ и z₂ делят окружность радиуса 4 на три равные части.

Углы между ними (2π/3)