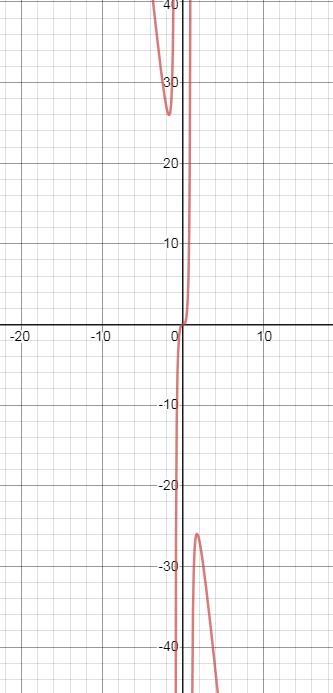
Задача 39781 Задание 7*. Исследование функции с...

danil_t

2019-09-23 12:13:15

Задание 7*. Исследование функции с помощью производной.
Для заданной функции провести полное исследование: точки разрыва функции, асимптоты, точки минимума, максимума, точки перегиба; интервалы возрастания, убывания функции, интервалы выпуклости и вогнутости функции. Построить график функции. На графике функции указать асимптоты, особые точки - точки экстремума, точки перегиба. Построение выполнить схематично на масштабно-координатной бумаге.

y = 10x^3 / (1 - x^2)

sova

2019-09-23 14:06:28

Область определения (- ∞ ;-1) U (-1;1) U(1;+ ∞ )

Исследование функции с помощью первой производной:

y`=10* ((x^3)`*(1-x^2)-x^3*(1-x^2)`)/(1-x^2)^2

y`=10*((3x^2*(1-x^2)-x^3*(-2x))/(1-x^2)^2

y`=10*(3x^2 - 3x^4 +2x^4)/(1 - x^2)^2

y`=10*(3x^2 - x^4)/(1 - x^2)^2

y`=0
3x^2 - x^4=0

x^2*(3- x^2)=0 ⇒
x^2 = 0 или x^2=3
x=0 или х = ± sqrt(3)

Знак производной:
__-___ (-sqrt(3)) _+_ (-1) __+__ (0) _+__ (1) __+__ (1sqrt(3)) __-__

y`>0 на (-sqrt(3); - 1) и на (-1;0) и на (0;1 ) и на (1; sqrt(3))

Функция монотонно возрастает

на (-sqrt(3); - 1) и на (-1;0) и на (0;1 ) и на (1; sqrt(3))


y` < 0 на (- ∞ ;-sqrt(3)) и на (sqrt(3);+ ∞ )

Функция монотонно убывает
на (- ∞ ;-sqrt(3)) и на (sqrt(3);+ ∞ )

x=-sqrt(3) -[b] точка минимума[/b]

y(-sqrt(3))=10*(-sqrt(3))^3/(1-(-sqrt(3))^2)= 15sqrt(3)

х=sqrt(3) - [b]точка максимума[/b]

y(sqrt(3))=10*(sqrt(3))^3/(1-(sqrt(3))^2)=-15sqrt(3)

Исследование функции с помощью второй производной:

y``=10*((3x^2 - x^4)/(1 - x^2)^2)`

y`=10*((3x^2-x^4)`*(1-x^2)^2-(3x^2-x^4)*((1-x^2)^2)`)/((1-x^2)^2)^2

y`=10*((6x-4x^3)*(1-x^2)^2-(3x^2-x^4)*2(1-x^2)*(1-x^2)`)/(1-x^2)^4

y`=10*2*x*(1-x^2)((3-2x^2)*(1-x^2)+3x^2-x^4)/(1-x^2)^4

y`=(x^4-2x^2+3)*x/(1-x^2)^3

y`=0

x^4-2x^2+3=0

D=4-4*3 <0

x=0 - [b]точка перегиба[/b], вторая производная меняет знак с + на -

y``>0 на (- ∞ ;-1) и (-1;0)
функция выпукла вниз на (- ∞ ;-1) и (-1;0)

y``< 0 на (0;1) U(1;+ ∞ )
функция выпукла вверх на (0;1) U(1;+ ∞ )