Задача 39718 7.18. Исследуйте на четность функцию:...
Условие
1) y = -6x+x^2 ...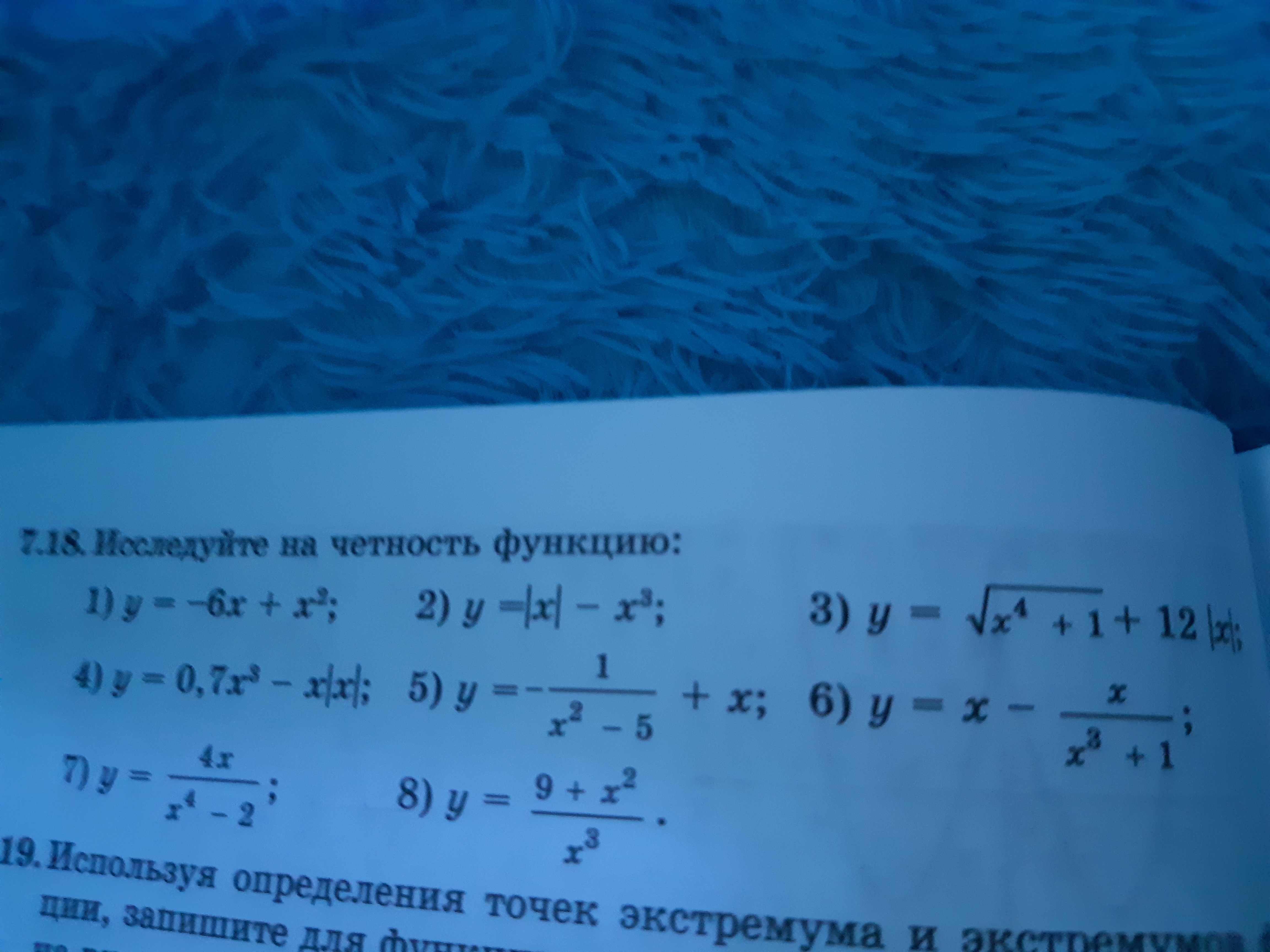
Решение
a) область определения функции симметрична относительно точки О;
б)
и f(-x)=f(x) для любого х из области определения, тогда функция чЁтная
f(-x)= - f(x) для любого х из области определения, тогда функция нечЁтная
1)
а) область определения функции (- ∞ ; + ∞ ) - симметрична относительно точки О;
б) f(-x)= -6*(-x)+(-x)^2=-6x+x^2
f(-x) ≠ f(x)
f(-x) ≠ - f(x)
[b]Функция не является ни чЁтной, ни нечЁтной
[/b]
2)
а) область определения функции (- ∞ ; + ∞ ) - симметрична относительно точки О;
б) f(-x)= |-x| -(-x)^3=|x|+x^3
f(-x) ≠ f(x)
f(-x) ≠ - f(x)
[b]Функция не является ни чЁтной, ни нечЁтной[/b]
3)
а) область определения функции (- ∞ ; + ∞ ) - симметрична относительно точки О;
б) f(-x)=sqrt((-x)^4+1)+12|-x|=sqrt(x^4+1)+12|x|
f(-x) = f(x)
[b]Функция является чЁтной[/b]
4)
а) область определения функции (- ∞ ; + ∞ ) - симметрична относительно точки О;
б) f(-x)= 0,7*(-x)^3-(-x)*|-x|=-0,7x^3+x*|x|=-(0,7x^3-x|x|)
f(-x) = - f(x)
[b]Функция является нечЁтной[/b]
5)
а) область определения функции (- ∞ ;-sqrt(5)) U (-sqrt(5);sqrt(5))U(sqrt(5); + ∞ ) - симметрична относительно точки О;
б) f(-x)= -[m]\frac{1}{(-x)^{2}-5}+(-x)= -\frac{1}{x^{2}-5}-x[/m]
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
[b]Функция не является ни чЁтной, ни нечЁтной[/b]
6)
а) область определения функции (- ∞ ;-1) U (-1; + ∞ ) - [b]НЕ[/b]симметрична относительно точки О;
не выполняется первый пункт определения, второй не проверяем!!!
[b]Функция не является ни чЁтной, ни нечЁтной[/b]
7)
а) область определения функции (- ∞ ;-sqrt(2)) U (-sqrt(2);sqrt(2))U(sqrt(2); + ∞ ) - симметрична относительно точки О;
б) f(-x)= [m]\frac{4\cdot (-x)}{(-x)^{4}-2}= -\frac{4x}{x^{4}-2}[/m]
f(-x) = f(x)
[b]Функция является чЁтной[/b]
8)
а) область определения функции (- ∞ ;0) U (0; + ∞ ) - симметрична относительно точки О;
б) f(-x)= [m]\frac{9+(-x)^{2}}{(-x)^{3}}= -\frac{9+x^{2}}{x^{3}}[/m]
f(-x) = - f(x)
[b]Функция является нечЁтной[/b]
