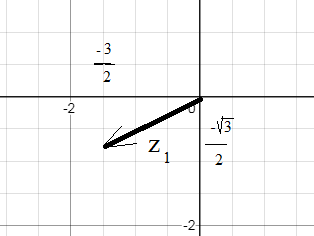Задача 39706 Даны комплексные числа z1 = -3/2 -...
Условие
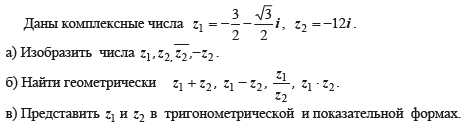
Все решения
Комплексное число z=x+iy изображают вектором с координатами (x;y)
Поэтому
z_(1)=([m]-\frac{3}{2};- \frac {\sqrt{3}}{2}[/m]) см. рис.1
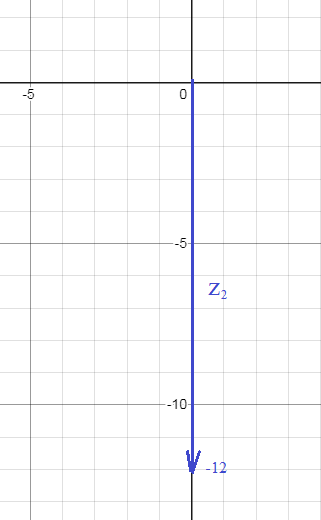
z_(2)=(0;-12) см. рис.2
vector{z_(2)}=12i
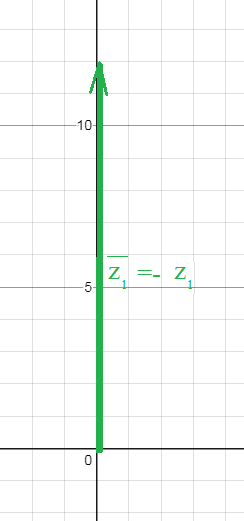
vector{z_(2)}=(0;12) см. рис. 3
-z_(2)=12i
-z_(2)=(0;12) см. рис. 3
б)
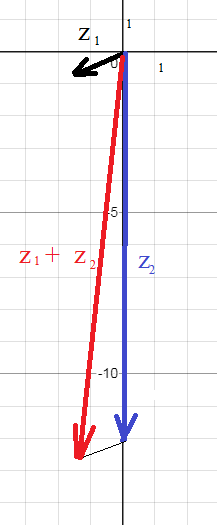
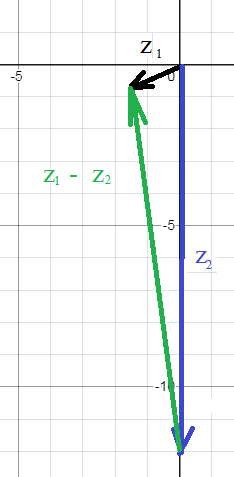
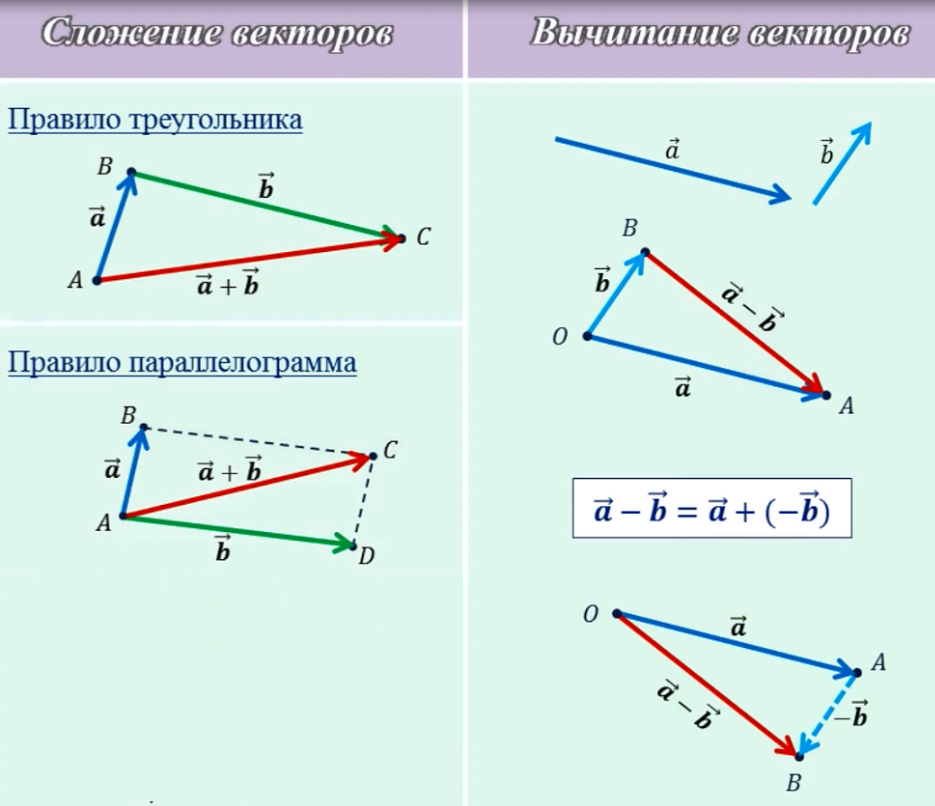
Применяем правило сложения векторов ( правило треугольника или правило параллелограмма см. последний рисунок). Геометрически см. рис. 4
Аналитически это так:
z_(1)+z_(2)= [m](-\frac{3}{2}- \frac {\sqrt{3}}{2}i)+ (-12i)=[/m]
= [m]-\frac{3}{2}- (\frac {\sqrt{3}}{2}+12)i=[/m]
= [m]-\frac{3}{2}- \frac {\sqrt{3}+24}{2}i[/m]
Применяем правило вычитания векторов ( правило треугольника или правило параллелограмма см. последний рисунок)
Геометрически см. рис. 5
Аналитически это так:
z_(1)- z_(2)= [m](-\frac{3}{2}- \frac {\sqrt{3}}{2}i)- (-12i)=[/m]
= [m]-\frac{3}{2}- (\frac {\sqrt{3}}{2}-12)i=[/m]
= [m]\frac{3}{2}- \frac {\sqrt{3}-24}{2}i[/m]
z_(1)*z_(2)= [m](-\frac{3}{2}- \frac {\sqrt{3}}{2}i)\cdot (-12i)=[/m]
[m]=12\cdot \frac{3}{2}i+12\cdot \frac {\sqrt{3}}{2}i^{2}=-6\sqrt{3}+18i[/m]
[m]\frac{z_{1}}{z_{2}}=\frac{-\frac{3}{2}- \frac {\sqrt{3}}{2}i}{-12i}=[/m]
умножаем и числитель и знаменатель на i
[m]=\frac{-\frac{3}{2}i- \frac {\sqrt{3}}{2}i^2}{-12i^2}=[/m]
[m]=\frac{-\frac{3}{2}i+ \frac {\sqrt{3}}{2}}{12}=[/m]
[m]=\frac {\sqrt{3}}{24}-\frac{3}{24}i=[/m]
[m]=\frac {\sqrt{3}}{24}-\frac{1}{8}i[/m]
в)
z=x+iy
|z|=sqrt(x^2+y^2)=
argz= φ
z=|z|*[m](cos\varphi +isin\varphi)[/m] - тригонометрическая форма комплексного числа z
z_(1)=[m](-\frac{3}{2}- \frac {\sqrt{3}}{2}i)[/m]
Запишем z_(1) в тригонометрической форме
[m]|z_{1}|=\sqrt{(-\frac{3}{2})^{2}+(-\frac {\sqrt{3}}{2})^{2}}=[/m]
=[m]\sqrt{\frac{9}{4}+\frac {3}{4}}=\sqrt{3}[/m]
argz_(1)= φ
sin φ =[m]\frac{y}{z_{1}}=\frac{-\frac{\sqrt{3}}{2}}{\sqrt{3}}=-\frac{1}{2}[/m]
cos φ =[m]\frac{x}{z_{1}}=\frac{-\frac{3}{2}}{\sqrt{3}}=-\frac{\sqrt{3}}{2}[/m]
φ =[m]-\frac{5\pi}{6}[/m]
z_(1)=[m]\sqrt{3}\cdot (cos(\frac{-5\pi}{6})+i\cdot sin(\frac{-5\pi}{6}))[/m] - тригонометрическая форма
Так как
[m]e^{i\varphi}=cos\varphi +isin\varphi[/m]
z_(1)=sqrt(3)*[m]e^{-\frac{5\pi}{6}\varphi}[/m]
z_(2)=-12I
|z_(2)|=12
sin φ =[m]\frac{y}{z_{2}}=\frac{-12}{12}=-1[/m]
cos φ =[m]\frac{x}{z_{1}}=\frac{0}{12}=0[/m]
φ =[m]-\frac{\pi}{2}[/m]
z_(2)=12*([m]cos(\frac{-\pi}{2})+i\cdot sin(\frac{-\pi}{2}))[/m] -
тригонометрическая форма
[m]e^{i\varphi}=cos\varphi +isin\varphi[/m]
Поэтому
z_(2)=[m]e^{-\frac{\pi}{2}i}[/m]