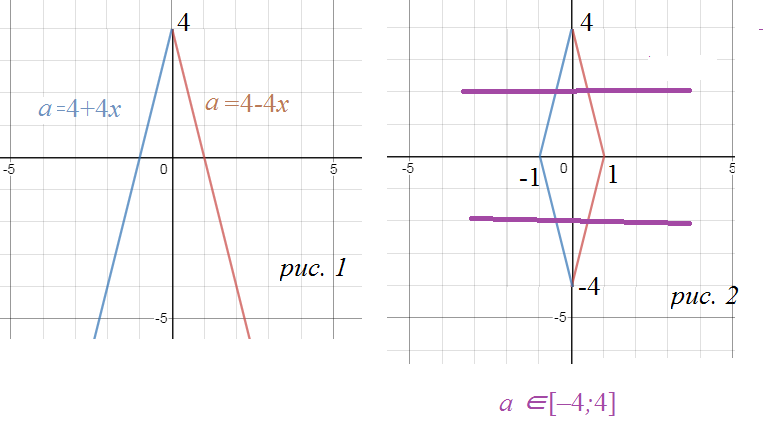Задача 39638 ...

slava191

2019-09-19 13:27:34

Найдите все значения а, при каждом из которых система неравенств

[m]\begin{cases} 4|x|+|a| ≤ 4 \\ x^2+2x ≤ a+3 \end{cases}[/m]

имеет хотя бы одно решение.

sova

2019-09-20 15:39:50

★

Перепишем первое неравенство системы:
|a| ≤ 4-4|x|

Рассмотрим координатно-параметрическую плоскость xOa:

Строим график |a|=4-4|x|
a=4-4x, x ≥ 0
a=4+4x, x <0

cм. рис. 1

Строим график |a|=4-4|x|

Отражаем часть графика на рис. 1 , расположенную выше оси Ох симметрично оси Ох

Получаем рис. 2

|a| ≤ 4-4|x| при a ∈ [-4;4]

Причем [green]это верно для x∈ [-1;1] [/green]



Перепишем второе неравенство системы:
x^2+2x -3 ≤ a

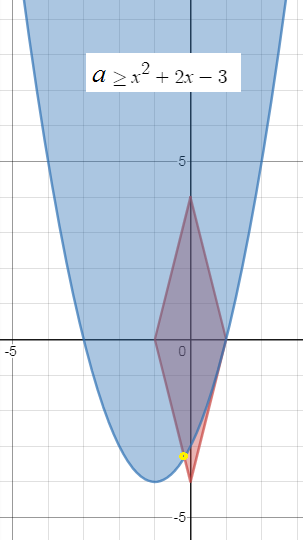
a ≥ x^2+2x-3
Этому множеству, удовлетворяют точки на плоскости, расположенные внутри параболы ( окрашено синим цветом)

Системе двух неравенств
{|a| ≤ 4-4|x| при a ∈ [-4;4]
{a ≥ x^2+2x-3
соответствует пересечение множеств

Найдем точку пересечения

a= - 4 - x и a=x^2+2x-3

x^2 + 2x - 3 = - 4 - x

x^2+3x+1=0

D=9-4=5

x=[m]\frac{-3\pm\sqrt{5}}{2}[/m]

x_(1)=[m]\frac{-3-\sqrt{5}}{2} > -1[/m]

x_(2)=[m]\frac{-3+\sqrt{5}}{2}[/m] [green]x∈ [-1;1] [/green] ⇒

a= - 4 - [m]\frac{-3+\sqrt{5}}{2}=\frac{-5-\sqrt{5}}{2}[/m]

О т в е т. ([m]\frac{-5-\sqrt{5}}{2}[/m]; 4]