Задача 39635 В конусе с вершиной S на окружности...

slava191

2019-09-19 13:20:42

В конусе с вершиной S на окружности основания отмечены точки М и К так что хорда МК перпендикулярна диаметру АВ. Длины дуг, на которые точки М и К делят окружность относятся как 1:5.

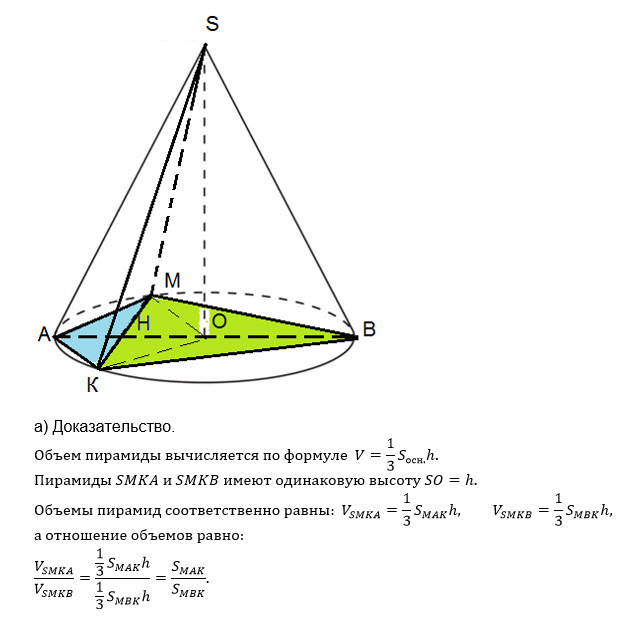
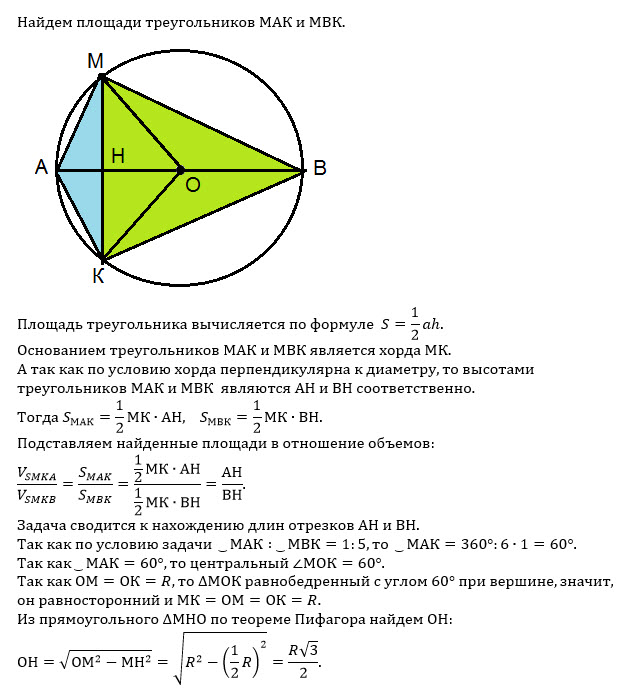
а) Докажите, что объёмы пирамид SMKA и SMKB относятся как [m]\frac{2-\sqrt3}{2+\sqrt3}[/m]

б) Найдите площадь сечения конуса плоскостью SMK, если радиус основания конуса равен 10, а длина образующей равна 13.