Задача 39476 4. Решая...

vk137953715

15 сентября 2019 г. в 15:20

4. Решая неравенство
[m]\frac{\log_{0,1}(2x+\frac{1}{4})}{ \lg(x^2 + 1)} \ge 0[/m]
на основе понятия «дробь неотрицательна, если…» ученик получил в ответе, что данное неравенство не имеет решения. Указать на ошибки в решении ученика (если таковые имелись). Привести верное решение по этому способу.

5. Исследовать функцию и построить ее график [m]y = 2\ln(x + 9) - 2x + 13[/m].

sova

16 сентября 2019 г. в 16:33

★

ОДЗ:
{2x+(1/4)>0 ⇒ x > –1/8
{lg(x²+1) ≠ 0 ⇒ x²+1 ≠ 1 ⇒ x² ≠ 0 ⇒ x ≠ 0

x ∈ (–1/8;0) U(0;+ ∞ )

Дробь неотрицательна...если числитель и знаменатель имеют одинаковые знаки ( с учетом второго неравенства ОДЗ, знаменатель не должен равняться 0) это приводит нас в двум системам неравенств:

1)
{log_0,1(2x+(1/4))≥0 ⇒ log_0,1(2x+(1/4)) ≥ log_0,11⇒ (2x+(1/4)) ≤ 1
{lg(x²+1) >0 ⇒ lg(x²+1) > lg1 ⇒ x²+1> 1 ⇒ x²>0 ⇒ x ≠ 0

или

2)
{log_0,1(2x+(1/4)) ≤ 0 ⇒ log_0,1(2x+(1/4)) ≤ log_0,11⇒ 2x+(1/4) ≥ 1
{lg(x²+1) <0 ⇒ lg(x²+1) < lg1 ⇒ x²+1< 1 ⇒ x²<0 – неравенство неверно при каких x, значит и вся система не имеет решений


Из 1)
{2x ≤ 1–(1/4) ⇒ x < ≤ 3/8
{x ≠ 0

С учетом ОДЗ получаем ответ
(–1/8;0) U (0;3/8]

2.
Область определения
x+9 >0 ⇒ x> – 9

Находим производную:

y`=[m]\frac{2}{x+9}-2[/m]

y`=0

[m]\frac{2}{x+9}-2=0[/m]

[m]\frac{2-2\cdot (x+9)}{x+9}=0[/m]

[m]\frac{2-2x -18}{x+9}=0[/m]

[m]\frac{-2x -16}{x+9}=0[/m]

–2x–16=0
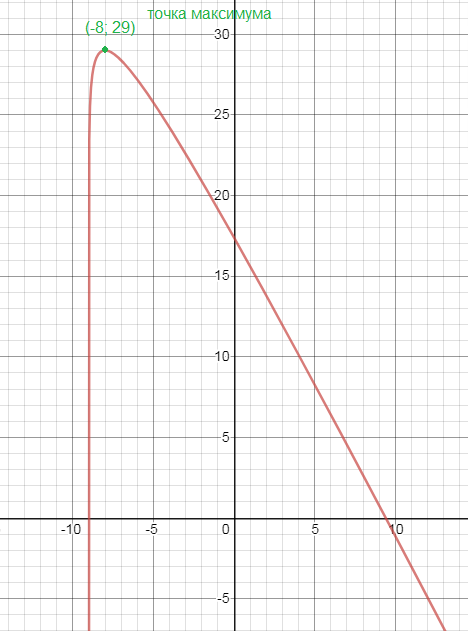
x=–8

Исследуем точку х=–8 на экстремум.

Проверяем знак производной при переходе через эту точку.
При x=–8,5
y`=(2/0,5)–2 >0, ставим + на интервале, содержащем точку (х=–8,5)т.е. на (–9;–8 )

(–9) _+_ (–8) ___–___

x=–8 – точка максимума, производная меняет знак с + на –

y(–8)=2ln1–2·(–8)+13=16+13=29 – наибольшее значение функции.


y``=[m]-\frac{2}{(x+9)^2}<0[/m] на ОДЗ

Кривая выпукла вверх