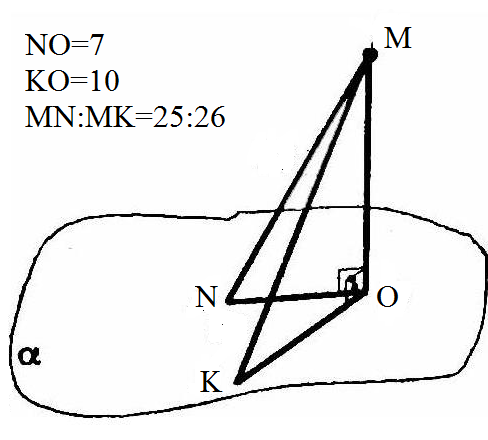
Задача 39452 ПОМОГИТЕ РЕШИТЬ...

vk306899767

2019-09-14 19:30:19

ПОМОГИТЕ РЕШИТЬ

sova

2019-09-14 19:54:44

Пусть x - коэффициент пропорциональности.
Тогда MN=25x; MK=26x

MO ⊥ пл. α

Проекция NO=7 ( меньшая наклонная имеет меньшую проекцию)
Проекция КO=10

По теореме Пифагора из прямоугольного треугольника MNO:
[green]MO^2[/green]=MN^2-NO^2=[red](25x)^2-7^2 [/red]

По теореме Пифагора из прямоугольного треугольника MKO:
[green]MO^2[/green]=MK^2-KO^2=[red](26x)^2-10^2 [/red]

Приравниваем правые части
(25x)^2-7^2=(26x)^2-10^2

10^2-7^2=(26x)^2-(25x)^2

100-49=(26x-25x)(26x+25x)
51=x*51x
x^2=1
x=1

О т в е т. MO=sqrt((25x)^2-7^2)
при x=1
MO=sqrt(25^2-7^2)=sqrt(576)=[b]24 см[/b]