Задача 39451 2.3. Чему равно наибольшее значение...

vk306899767

2019-09-14 19:24:32

2.3. Чему равно наибольшее значение функции f(x) = 1 + 3x^2 - x^3 на промежутке [-1; 1]?

sova

2019-09-14 19:40:05

★

f `(x) = (1+3x^2-x^3)`=6x-3x^2

f `(x)=0

6x-3x^2=0

3x(2-x)=0

x=0 или х=2

Знак производной

_-__ (0) __+__ (2) __-__

Отрезку [-1; 1] принадлежит только точка х=0

x=0 - точка минимума, так как производная меняет знак с - на +

Значит наибольшее значение на отрезке [-1;1] функция может принимать на одном из концов этого отрезка

f(-1)=1+3-(-1)^3=5
f(1)=1+3-1=3

[b]Наибольшее значение в точке х=-1 равно 5[/b]

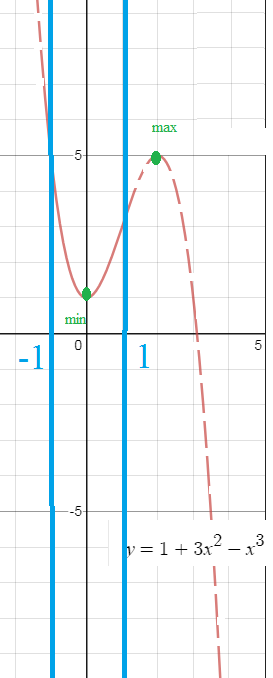
См. рис. Построен график у=1+3x^2-x^3

Интересует наибольшее значение внутри полосы от x=-1 до х=1