Задача 39364 Доказать на сходимость и найти сумму...
Условие
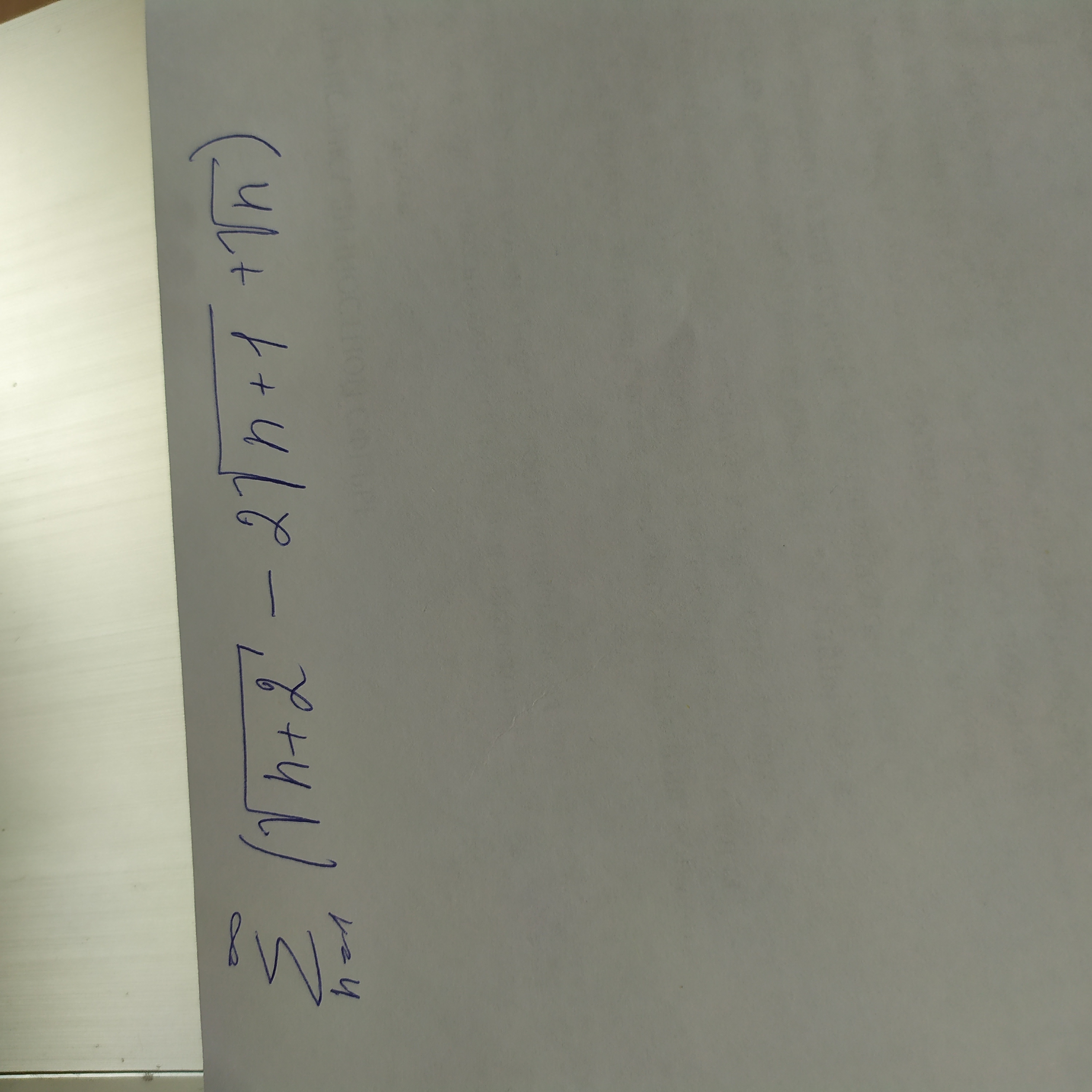
Все решения
+(sqrt(3+2)-2sqrt(3+1)+sqrt(3))+...+[blue](sqrt(n-2+2)-2sqrt(n-2+1)+sqrt(n-2))[/blue]+ [green](sqrt(n-1+2)-2sqrt(n-1+1)+sqrt(n-1))[/green]+[red](sqrt(n+2)-2sqrt(n+1)+sqrt(n))[/red]=
=-2sqrt(2)+sqrt(1)+sqrt(2)+sqrt(n-1+2)+sqrt(n+2)-2sqrt(n+1)=
=1-sqrt(2)+sqrt(n+2)-sqrt(n+1)
[m]\lim_{n \to\infty}S_{n}= \lim_{n \to\infty}(1-\sqrt{2}+\sqrt{n+2}-\sqrt{n+1})=[/m]
[m]=\lim_{n \to\infty}(1-\sqrt{2})+ \lim_{n \to\infty}(\sqrt{n+2}-\sqrt{n+1})=[/m]
[m]=(1-\sqrt{2})+ \lim_{n \to\infty}\frac{(\sqrt{n+2}-\sqrt{n+1})(\sqrt{n+2}+\sqrt{n+1})}{(\sqrt{n+2}+\sqrt{n+1})}=[/m]
[m]=(1-\sqrt{2})+ \lim_{n \to\infty}\frac{(n+2)-(n+1)}{(\sqrt{n+2}+\sqrt{n+1})}=[/m]
=[m](1-\sqrt{2})+ \lim_{n \to\infty}\frac{1}{(\sqrt{n+2}+\sqrt{n+1})}=1-\sqrt{2}+0=1-\sqrt{2}[/m]
Сходится по определению. Существует предел n-ой конечной суммы
