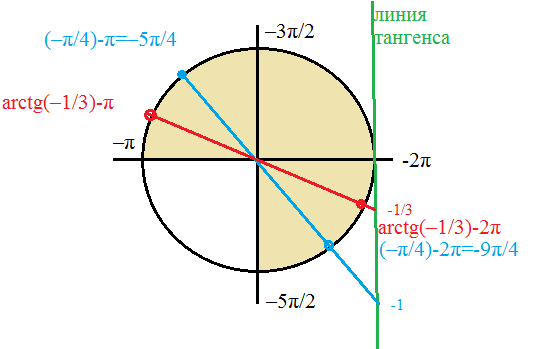Задача 39099 ...

bklg9999

2019-09-02 13:09:46

решить уравнение: cos2x-2sin2x=2
найти все корни уравнения принадлежащие отрезку [-5π/2;-π]

sova

2019-09-02 13:20:54

★

Так как
сos2x=cos^2x-sin^2x

sin2x=2sinxcosx

2=2*(cos^2x+sin^2x)

Получаем однородное тригонометрическое уравнение, сводящееся к квадратному:

3sin^2x+4sinxcosx+cos^2x=0

Делим на cos^2x ≠ 0

3tg^2x+4tgx+1=0

D=16-12=4

tgx= - 1 или tgx= - [m]\frac{1}{3}[/m]

x=-[m]\frac{π}{4}[/m]+πk, k ∈ Z или x=arctg(-[m]\frac{1}{3}[/m])+πn, n ∈ Z

О т в е т. а)
[red]x=-[m]\frac{π}{4}[/m]+πk, k ∈ Z[/red] или [red]x=arctg(-[m]\frac{1}{3}[/m])+πn, n ∈ Z[/red]
б) отбор корней:
при k=-2
x=-[m]\frac{π}{4}[/m]-2π = -[m]\frac{9π}{4}[/m] получаем первый корень, принадлежащий
отрезку.

при n=-2
x=arctg(-[m]\frac{1}{3}[/m])-2π получаем второй корень, принадлежащий
отрезку.

при k=-1
x=-[m]\frac{π}{4}[/m]-π= -[m]\frac{5π}{4}[/m]получаем третий корень, принадлежащий
отрезку.

при n=-1
x=arctg(-[m]\frac{1}{3}[/m])-π получаем четвертый корень, принадлежащий
отрезку.


cм. рис.