Задача 39090 5 и 6 пожалуйста помогите!!!!...

anzhela

2019-09-01 14:23:10

5 и 6 пожалуйста помогите!!!!

vk397114329

2019-09-01 20:50:48

5) z=-(i^53 2i^51)/(2 5i^37)
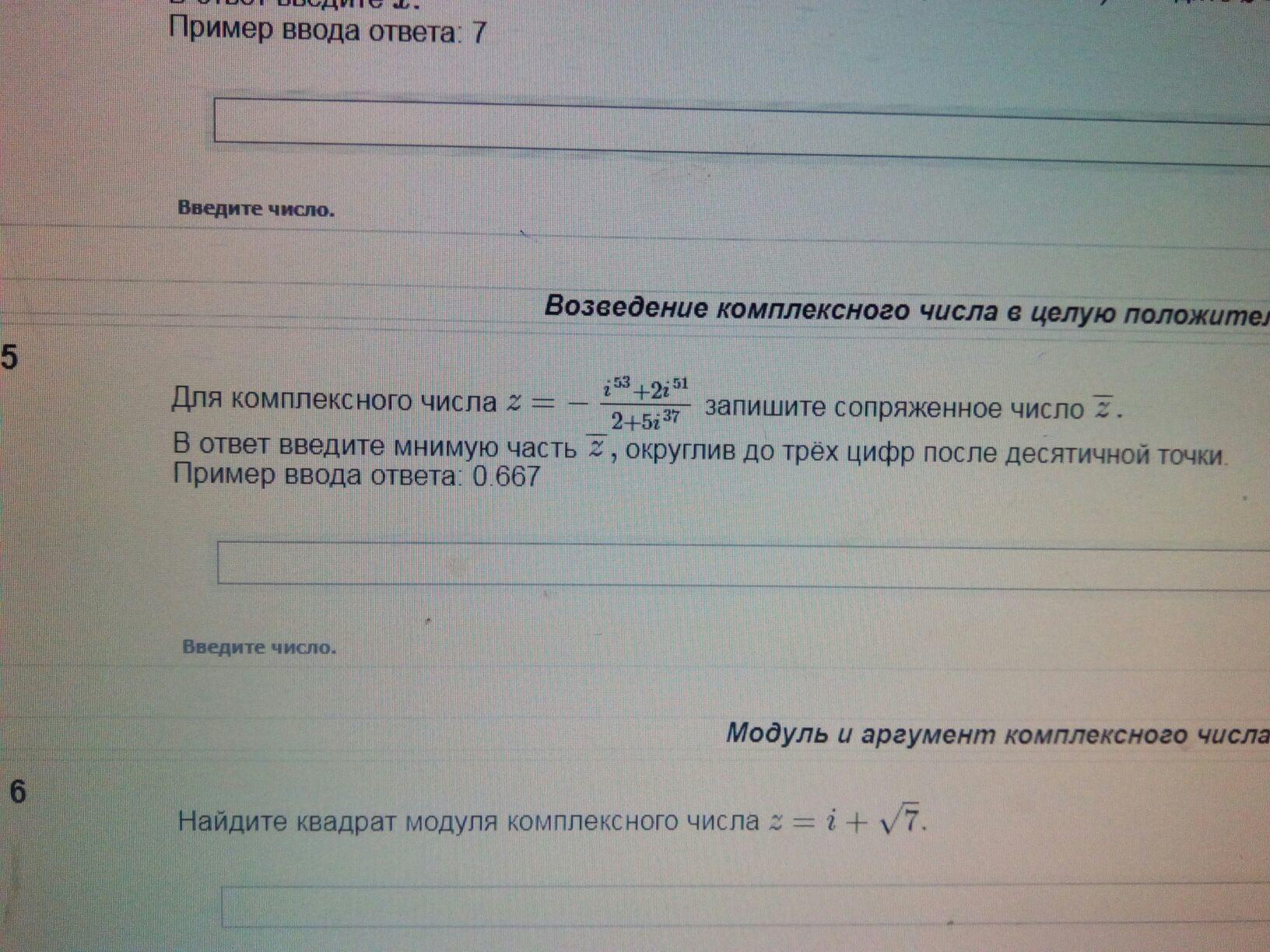
Решение:Мы знаем,что справедливы равенства:
i^2=-1; i^4k=1; i^(4k+ 1)=i; i^(4k +2)=-1; i^(4k +3)=-i.
где k ∈ z
В нашем примере i^53=i^(4*13+ 1)=i; i^51=i^(4*12+ 3)=-i; i^37=i^(4*9+ 1)=i.
Подставим найденные значения в исходное выражение и получим
z=-(i+ 2*(-i))/(2+ 5i)=-(i-2i)/(2+ 5i)=( i)/(2+ 5i). Умножим дробь на число сопряженное знаменателю
дроби получим z=(i*(2-5i))/(2+ 5i)(2-5i)=(2i-5i^2)/(4+ 25)=(5+ 2i)/29=5/29+ 2i/29=5/29+0.068i.
Сопряженное число имеет вид z'=5/29-0.068i.
Ответ:-0,068.
6)z=i sqrt(7)Модуль комплексного числа z=a+ bi называется число |z|=sqrt(a^2+ b^2) поэтому
|z|=sqrt(1+7)=sqrt(8) а |z|^2=8.
Ответ: 8.