Задача 39089 ...

anzhela

2019-09-01 14:22:38

3
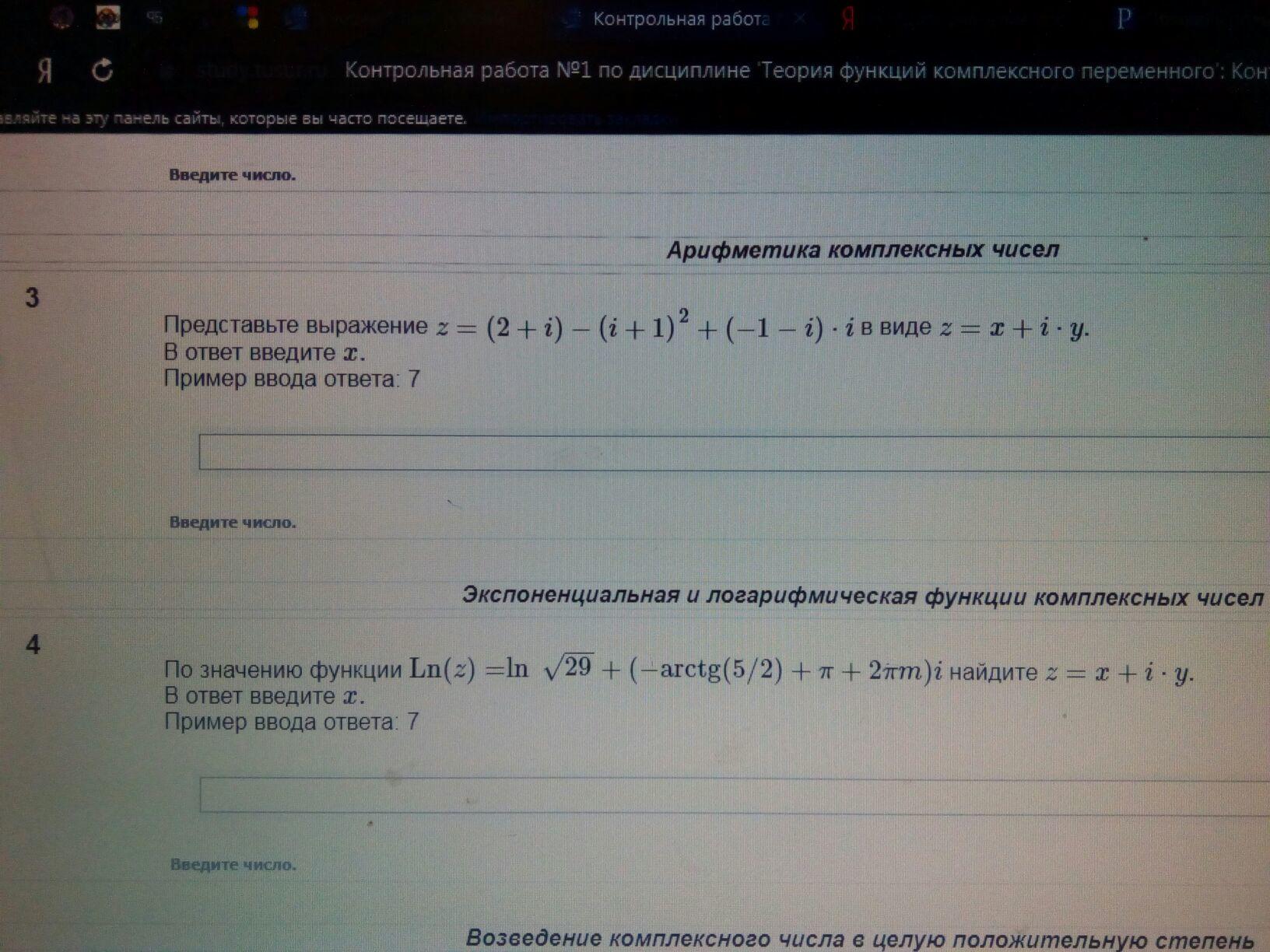
Представьте выражение z = (2 + i) - (i + 1) + (-1 - i) · i в виде z = x + i · y.
В ответ введите x.


4
По значению функции Ln(z) = ln √29 + ( - arctg(5/2) + π + 2πm)i найдите z = x + i · y.
В ответ введите x.

vk397114329

2019-09-01 23:57:56

3) z=(2+i)-(i+1)^2+(-1-i)*i=2+i-i^2-2i-1-i-i^2=
=1-2i-2i^2=1-2i+2=3-2i.
Ответ: 3
4) ln(z)=ln(sqrt(29))+( -arctq(5/2)+π +2πm)*i
По определению логарифма z=e^(ln(sqrt(29))+( -arctq(5/2)+π+2πm)*i
используем формулы:
1) e^(x+iy)=e^x(cosy+isiny)
2)sin(arctqx)=x/sqrt(1+x^2)
3)cos(arctqx)=1/sqrt(1+x^2)
4)cos(π-x)=-cosx
5)sin(π-x)=sinx
По формуле1 получаем z=e^sqrt(29)(( cos(-arctq(5/2)+π+2πm)+isin(-arctq(5/2)+π+2πm)
z=sqrt(29)((-cos(arctq(5/2)-isin(arctqq95/2))=sqrt(29)(-2/sqrt(29)-i*5/sqrt(29)=-2-5i.
Ответ: -2