Задача 39056 ...
Условие
математика 10-11 класс
666
Решение
★
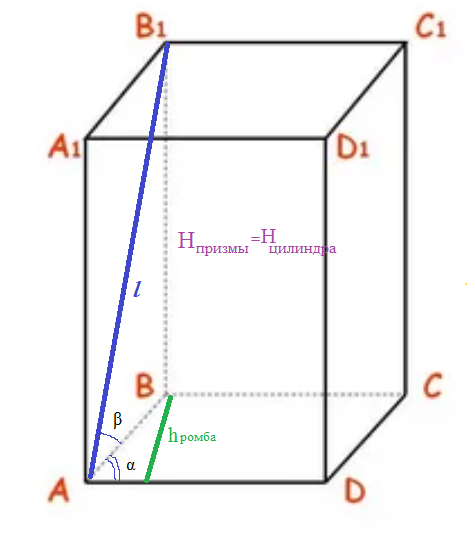
AB= [i]l[/i]*cos β
BB_(1)= [i]l[/i]*sinβ
H_(призмы)=Н_(цилиндра)= [i]l[/i]*sinβ
[i]h[/i]_(ромба)=[i]h [/i]= AB*sinα = [i]l[/i]*cosβ*sin α
r(окр. впис в ромб)=[m]\frac{h}{2}[/m]=[m]\frac{lcos\beta sin\alpha }{2}[/m]
S_(бок. пов. цилиндра)=2πr*H=
=[m]2\pi \frac{lcos\beta sin\alpha }{2}\cdot lsin\beta =\pi l^{2}sin\alpha sin\beta cos\beta =\frac{\pi l^{2}sin\alpha sin2\beta }{2}[/m]
О т в е т. [red][m]\frac{\pi l^{2}sin\alpha sin2\beta }{2}[/m][/red]