Задача 39045 Площадь основания ABC правильной...

velter

28 августа 2019 г. в 18:48

Площадь основания ABC правильной треугольной пирамиды ABCS равна 4 корень из 3 , а объем пирамиды равен 8 / корень 3 . Найдите боковое ребро пирамиды.

sova

28 августа 2019 г. в 20:09

S _{Δ ABC}=[m]\frac{a^{2}\sqrt{3}}{4}[/m], где а – сторона основания

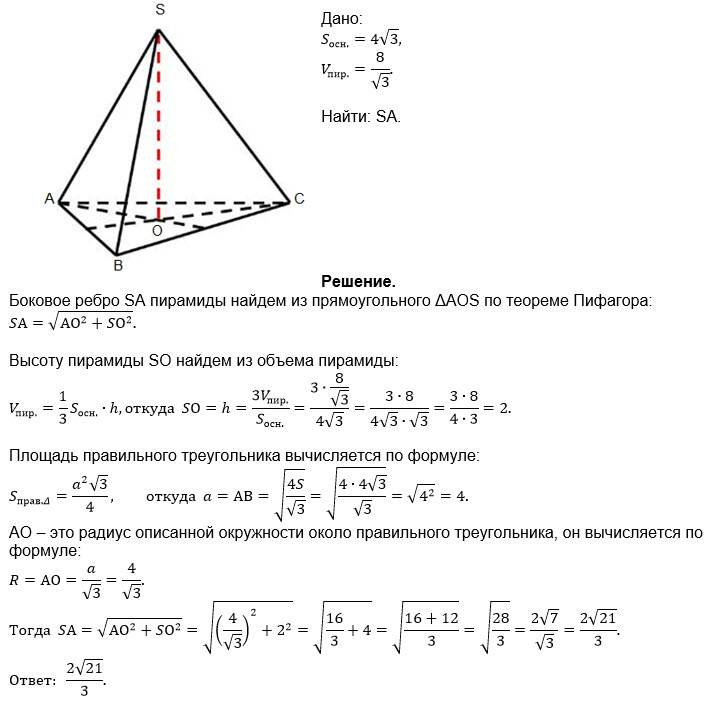
По условию
S _{Δ ABC}=4√3

[m]\frac{a^{2}\sqrt{3}}{4}[/m]=4√3 ⇒ а²=16 ⇒ a=4

V(пирамиды)=(1/3)·S_осн·Н

По условию
S_осн=4√3
V(пирамиды)=8/√3

(1/3)·(4√3)·Н=[m]\frac{8}{\sqrt{3}}[/m]


H=2

По теореме Пифагора
SA²=SO²+АО²

SO=H=2
AO=R=[m]\frac{a\sqrt{3}}{3}[/m]=[m]\frac{4\sqrt{3}}{3}[/m]


SA²=2²+([m]\frac{4\sqrt{3}}{3}[/m])²=4+([m]\frac{48}{9}[/m])=

=[m]\frac{84}{9}=\frac{28}{3}[/m]

[m]\sqrt{28}=\sqrt{4\cdot 7}=2\sqrt{7}[/m]

SA=[m]2\cdot \sqrt{\frac{7}{3}}[/m]

О т в е т. [m]2\cdot \sqrt{\frac{7}{3}}[/m]