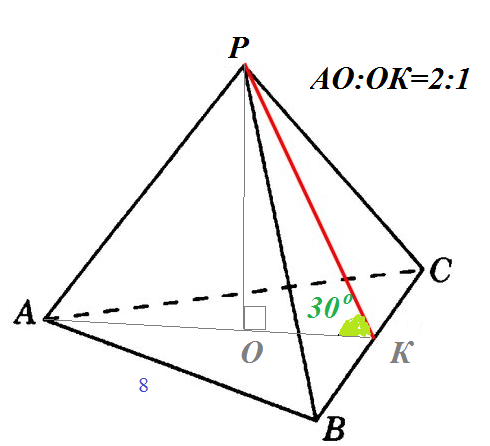
Задача 39015 2.4. Сторона основания правильной...

vk492803606

2019-08-27 10:52:22

2.4. Сторона основания правильной треугольной пирамиды равна 8 см, а боковая грань наклонена к плоскости основания под углом 30°. Найдите площадь полной поверхности пирамиды.

sova

2019-08-27 11:28:17

★

АК=h( Δ АВС)=8sqrt(3)/2=4sqrt(3)

ОК=(1/3)АК=4sqrt(3)/3

В прямоугольном треугольнике РОК
ОК=PK*cos30^(o)

РК=ОК/cos30^(o)=(4sqrt(3)/3) :(sqrt(3)/2)=(8/3)

Апофема боковой грани равна (8/3)

S_(пол)=3S_( ΔPAB)+S_( ΔABC)=

=(3*(1/2)*8*(8/3) + 8sqrt(3)/4=

= [b]32+2sqrt(3)[/b]