Задача 38977 ...
Условие
(x + 1)(x + 4)(x + 8)
──────-- ≥ -1.
(x - 1)(x - 4)(x - 8)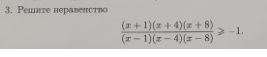
математика 10-11 класс
446
Решение
★
[b]([/b](x+1)(x+4)(x+8)+(x-1)(x-4)(x-8) [b])[/b]/(x-1)(x-4)(x-8) ≥ 0
[b]([/b](x^2+5x+4)(x+8)+(x^2-5x+4)(x-8) [b])[/b]/(x-1)(x-4)(x-8) ≥ 0
[b]([/b]x^3+5x^2+4x+8x^2+40x+32+x^3-5x^2+4x-8x^2+40x-32 [b])[/b]/(x-1)(x-4)(x-8) ≥ 0
(2x^3+88x)/(x-1)(x-4)(x-8) ≥ 0
2х(x^2+44)/(x-1)(x-4)(x-8) ≥ 0
x/(x-1)(x-4)(x-8) ≥ 0
Применяем метод интервалов:
_+__ [0] _-_ (1) ___+___ (4) ___-___ (8) ___+___
О т в е т. (- ∞ ;0] U(1;4)U(8;+ ∞ )